Δεκάγωνο

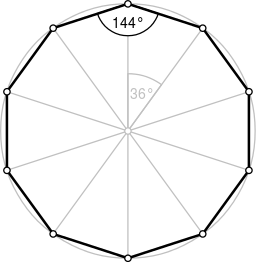
Στη γεωμετρία, το δεκάγωνο (από τις ελληνικές λέξεις δέκα και γωνία) είναι ένα οποιοδήποτε πολύγωνο σχήμα με δέκα πλευρές και δέκα κορυφές. Ωστόσο ο όρος συνήθως αναφέρεται σε ένα κανονικό δεκάγωνο, στο οποίο όλες οι πλευρές και όλες οι γωνίες είναι ίσες μεταξύ τους. Σε ένα τέτοιο δεκάγωνο, οι εσωτερικές γωνίες είναι ίσες με 144 μοίρες (°) η καθεμιά, ενώ οι εσωτερικές γωνίες οποιουδήποτε δεκαγώνου έχουν άθροισμα 1440 μοίρες ακριβώς. Το σύμβολο Schläfli του δεκαγώνου είναι {10}.

Κανονικό δεκάγωνο

Το εμβαδό (E) ενός κανονικού δεκαγώνου με μήκος πλευράς α δίνεται από τη σχέση:

\( {\displaystyle E={\frac {5}{2}}a^{2}\cot {\frac {\pi }{10}}={\frac {5a^{2}}{2}}{\sqrt {5+2{\sqrt {5}}}}\simeq 7,694208843a^{2}.} \)

Μία άλλη σχέση είναι E =5ad/2 , όπου d είναι η απόσταση μεταξύ παράλληλων πλευρών ή το ύψος του σχήματος όταν το δεκάγωνο στέκεται πάνω στη μία του πλευρά ως βάση.

Με απλούς τριγωνομετρικούς υπολογισμούς βρίσκουμε:

\( {\displaystyle d\,=\,2a(\cos {54^{\circ }}\,+\,\cos {18^{\circ }})}. \)

Πλευρές

Η πλευρά ενός κανονικού δεκαγώνου που είναι εγγεγραμμένο σε κύκλο ακτίνας 1 έχει μήκος:

\( {\displaystyle {\tfrac {-1+{\sqrt {5}}}{2}}={\tfrac {1}{\phi }}}, \) όπου φ είναι η «χρυσή αναλογία»,

\( {\displaystyle {\tfrac {1+{\sqrt {5}}}{2}}}. \)

Κατασκευή

Το κανονικό δεκάγωνο είναι δυνατό να κατασκευασθεί με κανόνα και διαβήτη:

Η κατασκευή ενός κανονικού δεκαγώνου

Μια εναλλακτική (αλλά παρόμοια) μέθοδος είναι η εξής:

Κατασκευάστε ένα κανονικό πεντάγωνο εγγεγραμμένο σε κύκλο με μία από τις μεθόδους που δίνονται στο αντίστοιχο λήμμα.
Εκτείνετε μία ευθεία από κάθε κορυφή του πενταγώνου διερχόμενη από το κέντρο του κύκλου προς την αντίθετη πλευρά. Το σημείο όπου η κάθε γραμμή τέμνει τον κύκλο απέναντι είναι μία κορυφή του δεκαγώνου.
Οι πέντε κορυφές του πενταγώνου είναι οι άλλες 5 κορυφές του δεκαγώνου. Ενώστε αυτά τα σημεία με τα νέα για να σχηματίσετε το (κανονικό) δεκάγωνο.

Παράγωγα σχήματα

Υπάρχει ένα κανονικό αστεροειδές πολύγωνο, γνωστό ως δεκάγραμμα, με σύμβολο Schläfli {10/3}, που προκύπτει από τις ίδιες κορυφές ενώνοντας μεταξύ τους κάθε τρίτη κορυφή. Επίσης, υπάρχουν δύο παραλλαγές: το {10/4} ανάγεται σε 2{5/2} ως δύο πενταγράμματα, και το {10/2} ανάγεται σε 2{5} ως δύο πεντάγωνα.

{10/3}
Decagram

{10/2} or 2{5}

{10/4} or 2{5/2}

Πολύγωνα Petrie

Το κανονικό δεκάγωνο είναι το πολύγωνο Πέτρι για πολλά πολύτοπα περισσότερων διαστάσεων, που παρατίθενται σε ορθογώνιες προβολές σε διάφορα επίπεδα Coxeter:

A₉	9-simplex	ανορθωμένο 9-simplex	διανορθωμένο 9-simplex	τριανορθωμένο 9-simplex	τετρανορθωμένο 9-simplex
BC₅	5-orthoplex	ανορθωμένο 5-orthoplex	διανορθωμένος 5-κύβος	ανορθωμένος 5-κύβος	5-κύβος
D₆	t₁(4₃₁)	t₃(1₃₁)	t₂(1₃₁)	t₁(1₃₁)	6-ημίκυβος (1₃₁)
H₃	δωδεκάεδρο Πέτρι	εικοσάεδρο Πέτρι	εικοσιδωδεκάεδρο