.
Στα Μαθηματικά και την τέχνη, δύο ποσότητες έχουν αναλογία χρυσής τομής αν ο λόγος του αθροίσματος τους προς τη μεγαλύτερη ποσότητα είναι ίσος με το λόγο της μεγαλύτερης ποσότητας προς τη μικρότερη. Η εικόνα στα δεξιά αναπαριστά τη γεωμετρική ερμηνεία των παραπάνω. Εκφρασμένο αλγεβρικά:
\frac{a+b}{a} = \frac{a}{b} \ \stackrel{\text{def}}{=}\ \varphi,
όπου το γράμμα \varphi αντιπροσωπεύει την χρυσή τομή. Η τιμή του είναι:
\varphi = \frac{1+\sqrt{5}}{2} = 1.61803\,39887\ldots.
Η χρυσή τομή αναφέρεται επίσης και ως χρυσός λόγος ή χρυσός κανόνας. Άλλα ονόματα είναι χρυσή μετριότητα και Θεϊκή αναλογία ενώ στον Ευκλείδη ο όρος ήταν "άκρος και μέσος λόγος".
Πολλοί καλλιτέχνες και αρχιτέκτονες του 20ου αιώνα προσάρμοσαν τα έργα τους ώστε να προσεγγίζουν την χρυσή αναλογία—ιδίως στη μορφή του χρυσού ορθογωνίου παραλληλογράμμου, στο οποίο ο λόγος της μεγαλύτερης πλευράς προς την μικρότερη είναι η χρυσή τομή—πιστεύοντας ότι αυτή η αναλογία είναι αισθητικά ευχάριστη. Οι Μαθηματικοί από την εποχή του Ευκλείδη μέχρι σήμερα έχουν μελετήσει τις ιδιότητες της χρυσής τομής, συμπεριλαμβανομένης της εμφάνισης της στις διαστάσεις ενός κανονικού πενταγώνου και ενός χρυσού ορθογωνίου παραλληλογράμμου, το οποίο (όπως φαίνεται και στην διπλανή εικόνα) μπορεί να χωριστεί σε ένα τετράγωνο και ένα παρόμοιο παραλληλόγραμμο με τον ίδιο λόγο πλευρών όπως το αρχικό. Η χρυσή τομή έχει χρησιμοποιηθεί επίσης για την ανάλυση των αναλογιών φυσικών αντικειμένων καθώς και τεχνητών συστημάτων όπως οι οικονομικές αγορές.
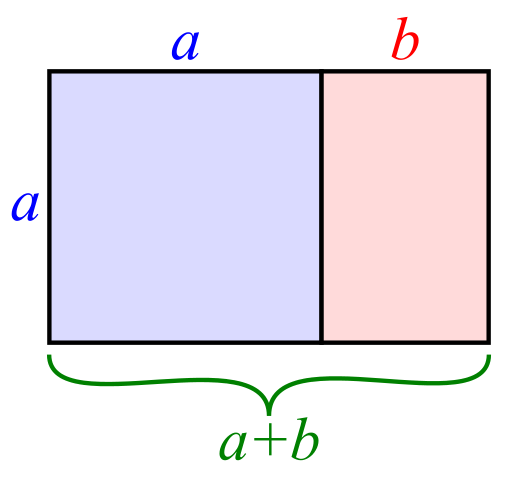
Ένα ορθογώνιο παραλληλόγραμμο με αναλογίες χρυσής τομής, με μεγαλύτερη την πλευρά a και μικρότερη την πλευρά b, όταν τοποθετείται δίπλα σε ένα τετράγωνο με πλευρές μήκους a, θα παραχθεί ένα όμοιο ορθογώνιο παραλληλόγραμμο με αναλογίες χρυσής τομής με μεγαλύτερη πλευρά την a + b και μικρότερη την a. Αυτό αναπαριστά η σχέση \frac{a+b}{a} = \frac{a}{b} \equiv \varphi. .
Υπολογισμός
Πρότυπο:Άρρητος αριθμός
Δυαδικό σύστημα 1.1001111000110111011...
Δεκαδικό σύστημα 1.6180339887498948482...
Δεκαεξαδικό σύστημα 1.9E3779B97F4A7C15F39...
Συνεχές κλάσμα 1 + \cfrac{1}{1 + \cfrac{1}{1 + \cfrac{1}{1 + \cfrac{1}{1 + \ddots}}}}
Αλγεβρικός αριθμός \frac{1 + \sqrt{5}}{2}
Άπειρη σειρά \frac{13}{8}+\sum_{n=0}^{\infty}\frac{(-1)^{(n+1)}(2n+1)!}{(n+2)!n!4^{(2n+3)}}
Δύο ποσότητες α και β λέγεται ότι είναι σε χρυσή αναλογία φ, εάν:
\frac{a+b}{a} = \frac{a}{b} = \varphi.
Μία μέθοδος για την εύρεση της τιμής του φ είναι να ξεκινήσουμε με το αριστερό κλάσμα. Με απλοποίηση του κλάσματος και αντικαθιστώντας το b / a = 1 / φ,
\frac{a+b}{a} = 1 + \frac{b}{a} = 1 + \frac{1}{\varphi},
φαίνεται ότι
1 + \frac{1}{\varphi} = \varphi.
Πολλαπλασιάζοντας με φ παίρνουμε ότι
\varphi + 1 = \varphi^2
το οποίο μπορεί να διαμορφωθεί σε
{\varphi}^2 - \varphi - 1 = 0.
Χρησιμοποιώντας την φόρμουλα επίλυσης δευτεροβάθμιων εξισώσεων, λαμβάνουμε δύο λύσεις:
\varphi = \frac{1 + \sqrt{5}}{2} = 1.61803\,39887\dots
και
\varphi = \frac{1 - \sqrt{5}}{2} = -0.6180\,339887\dots
Επειδή το φ είναι η αναλογία μεταξύ θετικών ποσοτήτων, το φ είναι απαραιτήτως θετικό:
\varphi = \frac{1 + \sqrt{5}}{2} = 1.61803\,39887\dots
Ιδιότητες
Από την παραπάνω εξίσωση προκύπτει \,\phi=1+1/\phi σύμφωνα με την οποία μπορούμε να εκφράσουμε το \(\,\phi ως άπειρο συνεχές κλάσμα:
\,\phi=1+\frac1{\phi}=1+\frac1{1+\frac1{\phi}}=\cdots=1+\frac1{1+\frac1{1+\frac1{1+\frac1{\dots}}}}
Το \,\phi αποτελεί το όριο του πηλίκου δύο διαδοχικών αριθμών Φιμπονάτσι.
Κατασκευή με κανόνα και διαβήτη
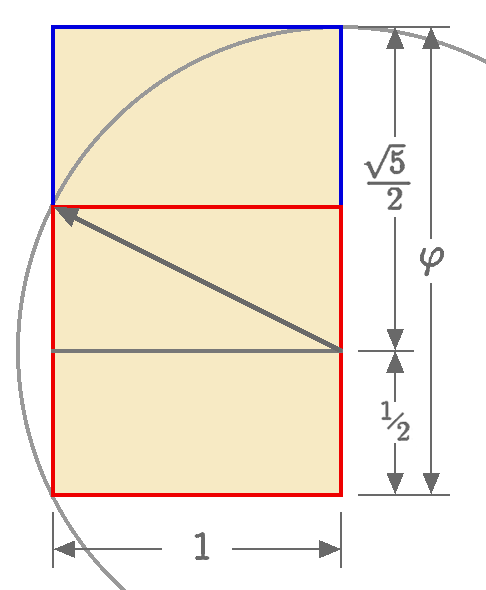
1. Κατασκευάζουμε τετράγωνο πλευράς 1 (κόκκινο).
2. Φέρουμε ευθεία παράλληλη προς τη μια βάση και χωρίζουμε το τετράγωνο σε δύο ίσα ορθογώνια (πλευρών 1 και 1/2) και φέρνουμε μία διαγώνιο (γκρι).
3. Κατασκευάζουμε κύκλο με κέντρο το μέσο της μίας πλευράς του τετραγώνου και ακτίνα τη διαγώνιο του ορθογωνίου.
4. Προεκτείνουμε την πλευρά του τετραγώνου στην οποία έχουμε ορίσει το κέντρο του κύκλου έως το σημείο του κύκλου που τελειώνει η διάμετρος
Το ευθύγραμμο τμήμα που αποτελείται από την πλευρά του τετραγώνου μαζί με την προέκταση έχει μήκος φ.
Ιστορία
Το σήμα των Πυθαγορείων μαζί με την επισήμανση του χρυσού λόγου
O Μαθηματικός Mark Barr πρότεινε να χρησιμοποιείται το πρώτο γράμμα του γλύπτη Φειδία για τον συμβολισμό της χρυσής τομής. Συνήθως χρησιμοποιείται το "μικρό" γράμμα φ. Κάποιες φορές το κεφαλαίο Φ χρησιμοποιείται για τον αντίστροφο της χρυσής τομής 1/φ.
Ο Michael Maestlin πρώτος δημοσίευσε μια δεκαδική προσέγγιση της χρυσής τομής, το 1597.
Η χρυσή τομή συνεπαίρνει Δυτικούς διανοούμενους ποικίλων ενδιαφερόντων για τουλάχιστον 2.400 χρόνια.
Οι Αρχαίοι Έλληνες μαθηματικοί πρώτοι μελέτησαν αυτό που τώρα ονομάζουμε χρυσή τομή γιατί εμφανιζόταν συχνά στη γεωμετρία. Η διαίρεση ενός τμήματος σε "άκρο και μέσο λόγο" (εξ ού και η χρυσή τομή) είναι σημαντική στη γεωμετρία των πενταγράμμων και πενταγώνων. Η αντίληψη αυτή αποδίδεται συνήθως στον Πυθαγόρα και τους ακολούθους του.
Ο χρυσός λόγος ήταν γνωστός στους Πυθαγόρειους. Στο μυστικό τους σύμβολο, την πεντάλφα, ο χρυσός λόγος εμφανίζεται στις πλευρές τους αστεριού καθώς και στο πηλίκο του εμβαδού του κανονικού πενταγώνου με κορυφές τις άκρες της πεντάλφα προς το εμβαδόν του κανονικού πενταγώνου που σχηματίζεται εντός του αστεριού.
Τα Στοιχεία του Ευκλείδη παρέχουν τον πρώτο γραπτό ορισμό αυτού που σήμερα ονομάζουμε χρυσή τομή: "Μια ευθεία γραμμή λέγεται ότι έχει κοπεί σε άκρο και μέσο λόγο, όταν όλη η ευθεία είναι για το μεγαλύτερο κομμάτι ότι είναι το μεγαλύτερο κομμάτι για το μικρότερο". Ο Ευκλείδης παραθέτει μια για το χώρισμα της γραμμής σε "άκρο και μέσο λόγο". Σε όλα τα Στοιχεία αρκετές προτάσεις και οι αποδείξεις τους εμπεριέχουν τον χρυσό λόγο.
Η πρώτη γνωστή προσέγγιση του (αντίστροφου) χρυσού λόγου από δεκαδικό κλάσμα, ως "περίπου 0,6180340", γράφτηκε το 1597 από τον Michael Maestlin του Πανεπιστήμιο του Τύμπιγκεν σε ένα γράμμα του προς τον πρώην φοιτητή του Γιοχάνες Κέπλερ.
Από τον 20ο αιώνα, η χρυσή τομή παριστάνεται με τον ελληνικό γράμμα Φ ή φ (φ, από το αρχικό γράμμα του γλύπτη Φειδία ο οποίος λέγεται ότι ήταν από τους πρώτους που τον χρησιμοποίησε στα έργα του) και πιο σπάνια από το τ το αρχικό γράμμα της λέξης τομή.
Χρονολόγιο
Χρονολόγιο σύμφωνα με τον Priya Hemenway:[1]
Ο Φειδίας (490–430 π.Χ.) έφτιαξε τα αγάλματα του Παρθενώνα τα οποία φαίνεται να ενσωματώνουν την χρυσή αναλογία.
Ο Πλάτων (427–347 π.Χ.), στον Τίμαιο, περιγράφει τα πέντε Πλατωνικά στερεά: το τετράεδρο, τον κύβο, το οκτάεδρο, το δωδεκάεδρο, και το εικοσάεδρο), κάποια από τα οποία σχετίζονται με την χρυσή τομή.[2]
Ο Ευκλείδης (π. 325–π. 265 π.Χ.), στα Στοιχεία, έδωσε τον πρώτο γραπτό ορισμό της χρυσής τομής, την οποία ονόμασε "ἄκρος καὶ μέσος λόγος"
Ο Φιμπονάτσι (1170–1250) ανέφερε την ακολουθία αριθμών που τώρα φέρει το όνομα του στο βιβλίο του Liber Abaci; ο λόγος διαδοχικών στοιχείων της ακολουθίας Φιμπονάτσι προσεγγίζει ασυμπτωτικά την χρυσή τομή.
Ο Λούκα Πατσιόλι (Luca Pacioli, 1445–1517) καθορίζει την χρυσή τομή ως "Θεϊκή αναλογία" στο ομώνυμο έργο του Divina Proportione.
Ο Μίχαελ Μαίστλιν (Michael Maestlin, 1550–1631) δημοσιεύει την πρώτη γνωστή προσέγγιση του (αντίστροφου) χρυσού λόγου από δεκαδικό κλάσμα.
Ο Γιοχάνες Κέπλερ (1571–1630) αποδεικνύει ότι η χρυσή τομή είναι το όριο της ακολουθίας των λόγων διαδοχικών όρων της ακολουθίας Φιμπονάτσι,[3] (\lim_{n\to\infty}\frac{F_{n+1}}{F_n}=\varphi) και περιγράφει την χρυσή τομή ως "πολύτιμο κόσμημα": "Η Γεωμετρία έχει δύο θησαυρούς: ο ένας είναι το Πυθαγόρειο Θεώρημα, και ο άλλος η τμήση μιας ευθείας σε άκρο και μέσο λόγο· τον πρώτο μπορούμε να τον συγκρίνουμε με χρυσό, τον δεύτερο με ένα πολύτιμο κόσμημα." οι δύο αυτοί θησαυροί συνδυάζονται στο Τρίγωνο του Κέπλερ.
Ο Charles Bonnet (1720–1793) επισημαίνει ότι στη φυλλοταξία φυτών που πηγαίνουν με την φορά των δεικτών του ρολογιού και αντίστροφα υπήρχαν συχνά δύο διαδοχικές ακολουθίες Φιμπονάτσι.
Ο Martin Ohm (1792–1872) πιστεύεται ότι είναι ο πρώτος που χρησιμοποίησε τον όρο goldener Schnitt (χρυσή τομή) για να περιγράψει αυτό το λόγο, το 1835.[4]
Ο Édouard Lucas (1842–1891) δίνει στην ακολουθία που τώρα είναι γνωστή ως Φιμπονάτσι το σημερινό της όνομα.
Ο Mark Barr (20ος αιώνας) προτείνει το ελληνικό γράμμα φ, το πρώτο γράμμα του γλύπτη Φειδία για τον συμβολισμό της χρυσής τομής.[5]
Ο Ρότζερ Πένροουζ (γεν. 1931) ανακάλυψε ένα συμμετρικό μοτίβο που χρησιμοποιεί την χρυσή τομή στο πεδίο των απεριοδικών πλακοστρώσεων.
Εφαρμογές και παρατηρήσεις
Αισθητική
Το De Divina proportione, ένα τρίτομο έργο του Luca Pacioli, δημοσιεύθηκε το 1509.Ο Pacioli, ένας Φραγκισκανός μοναχός, ήταν κυρίως γνωστός ως μαθηματικός, αλλά είχε επίσης εκπαιδευτεί και έδειχνε έντονο ενδιαφέρον για την τέχνη.Στο De Divina proportione διερευνήθηκαν τα μαθηματικά της χρυσής αναλογίας.Παρ'ότι λέγεται συχνά ότι ο Pacioli υποστήριζε την εφαρμογή της χρυσή αναλογίας για να δώσει ευχάριστες, αρμονικές αναλογίες,ο Livio επισημαίνει ότι η ερμηνεία έχει προήλθε από ένα λάθος το 1799, και ότι ο Pacioli υποστήριζε πραγματικά το Βιτρούβιο σύστημα των ρητών αναλογιών.[6] Ο Pacioli επίσης παρατήρησε θρησκευτική σημασία στην αναλογία, η οποία οδήγησε στον τίτλο του έργου του. Το De Divina proportione περιλαμβάνει απεικονίσεις των κανονικών στερεών από τον Leonardo da Vinci, παλιό φίλο και συνεργάτη του Pacioli.
Αρχιτεκτονική
Πολλές από τις αναλογίες του Παρθενώνα φέρονται να εμφανίζουν την χρυσή αναλογία
Η πρόσοψη του Παρθενώνα, καθώς και τα στοιχεία της πρόσοψης αυτού λέγεται από κάποιους ότι οριοθετήθηκαν από ορθογώνια με χρυσές αναλογίες.[7] Άλλοι μελετητές αρνούνται ότι οι Έλληνες είχαν κάποια αισθητική συσχέτιση με τη χρυσή αναλογία. Για παράδειγμα,ο Midhat J. Gazale λέει, "...Ωστόσο, έπρεπε να φτάσουμε στον Ευκλείδη προκειμένου να μελετηθούν οι μαθηματικές ιδιότητες της χρυσής τομής. Στα Στοιχεία (308 π.Χ.), ο Έλληνας μαθηματικός απλώς θεωρούσε τον αριθμό αυτό ως έναν ενδιαφέροντα άρρητο αριθμό, σε σχέση με τις μεσαίες και ακραίες αναλογίες. Η εμφάνιση του σε κανονικά πεντάγωνα και δεκάγωνα ήταν δεόντως σεβαστή, καθώς επίσης και στο δωδεκάεδρο (ένα κανονικό πολύεδρο που έχει ως έδρες δώδεκα κανονικά πεντάγωνα ). Είναι πράγματι υποδειγματικό ότι ο μεγάλος Ευκλείδης, σε αντίθεση με τις γενιές των μυστικιστών που ακολούθησαν, αντιμετώπισε με νηφαλιότητα τον αριθμό αυτό για αυτό που είναι, χωρίς να προσκολλήσει σε αυτόν άλλες από τις πραγματικές του ιδιότητές." [8] Και ο Κηθ Ντέβλιν, λέει," Σίγουρα, ο συχνά επαναλαμβανόμενος ισχυρισμός ότι ο Παρθενώνας στην Αθήνα βασίζεται στη χρυσή αναλογία δεν υποστηρίζεται από τις πραγματικές μετρήσεις. Στην πραγματικότητα, ολόκληρη η ιστορία για τους Έλληνες και την χρυσή αναλογία φαίνεται να είναι αβάσιμη.Το μόνο πράγμα που γνωρίζουμε με βεβαιότητα είναι ότι ο Ευκλείδης, στο περίφημο βιβλίο του Στοιχεία , που γράφτηκε γύρω στο 300 π.Χ., έδειξε πώς υπολογίζεται η τιμή της χρυσής αναλογίας ".[9] Εγγύς πηγές της εποχής, όπως ο Βιτρούβιος συζητούν αποκλειστικά αναλογίες που μπορούν να εκφραστούν σε ακέραιους αριθμούς. Ο Π. Φουτάκης μελέτησε τις διαστάσεις 15 αρχαίων ναών, 18 μνημειακών τάφων, 8 σαρκοφάγων και 58 επιτύμβιων στηλών γιά το διάστημα από τον 5ο αιώνα π.Χ. μέχρι τον 2ο αιώνα μ.Χ. Οι αρχαίοι ναοί αποτελούσαν το κατεξοχήν μέρος επικοινωνίας μεταξύ ανθρώπων και θεών, ενώ οι τάφοι, σαρκοφάγοι και επιτύμβιες στήλες συνδέονταν με το πέρασμα των θνητών από την υλική στην αιώνια ζωή. Εάν η χρυσή τομή είχε οποιεσδήποτε θεικές, μυστικιστικές ή αισθητικές ιδιότητες, τότε οι περισσότερες από αυτές τις κατασκευές θα χαρακτηρίζονταν από τον κανόνα της χρυσής αναλογίας. Το αποτέλεσμα αυτής της πρωτότυπης έρευνας είναι ξεκάθαρο: η χρυσή τομή ήταν εντελώς απούσα από την ελληνική αρχιτεκτονική του κλασικού 5ου αιώνα π.Χ., και σχεδόν απούσα για τους επόμενους έξι αιώνες. Τέσσερα σπάνια, και για αυτό πολύτιμα, παραδείγματα εφαρμογής αναλογιών χρυσής τομής εντοπίσθηκαν σε ένα αρχαίο πύργο της Μεθώνης Μεσσηνίας, στο Μεγάλο Βωμό της Περγάμου (στο ομώνυμο μουσείο του Βερολίνου), σε μια επιτύμβια στήλη από την Έδεσσα και σε ένα μνημειακό τάφο στην Πέλλα. Είναι η πρώτη φορά που παρουσιάζεται απόδειξη για εφαρμογή χρυσής τομής σε αρχαία ελληνική κατασκευή, ωστόσο, σύμφωνα με το συγγραφέα, εφαρμογή περιθωριακή η οποία υποδηλώνει ότι οι αρχαίοι Έλληνες δεν έδωσαν ιδιαίτερη σημασία στη χρυσή τομή στο χώρο της αρχιτεκτονικής.[10]
Μία γεωμετρική ανάλυση προηγούμενης έρευνας το 2004 για το Μεγάλο Τζαμί της Καϊρουάν αποκαλύπτει μια συνεπή εφαρμογή της χρυσής αναλογίας σε όλο το σχεδιασμό, σύμφωνα με τον Boussora και τον Mazouz.[11] Βρήκαν αναλογίες κοντά στη χρυσή στο συνολικό ποσοστό του σχεδίου καθώς και στο χώρο προσευχής και στο χώρο του δικαστηρίου . Οι συντάκτες σημειώνουν, ωστόσο, ότι οι περιοχές που βρέθηκαν να έχουν αναλογίες κοντά στην χρυσή δεν αποτελούν μέρος της αρχικής κατασκευής, και θεωρούν ότι αυτά τα στοιχεία προστέθηκαν σε μια ανακατασκευή.
Ο Ελβετός αρχιτέκτονας Λε Κορμπυζιέ, γνωστός για τη συμβολή του στο σύγχρονο διεθνές αρχιτεκτονικό στυλ, εστίασε τη φιλοσοφία του σχεδιασμού του σε συστήματα αρμονίας και αναλογίας. Η πίστη του Λε Κορμπυζιέ στη μαθηματική τάξη του σύμπαντος ήταν στενά συνδεδεμένη με τη χρυσή αναλογία και τη σειρά Φιμπονάτσι, τις οποίες περιέγραψε ως "ρυθμούς εμφανείς δια γυμνού οφθαλμού και σαφείς στις σχέσεις τους το ένα με το άλλο. Και αυτοί οι ρυθμοί βρίσκονται στη ρίζα των ανθρωπίνων δραστηριοτήτων. Αντηχούν στον άνθρωπο από οργανικό αναπόφευκτο, το ίδιο αναπόφευκτο που προκαλεί την παρατήρηση της Χρυσής Τομής από τα παιδιά, τους ηλικιωμένους, τους άγριους και τους μορφωμένους ".[12]
Ο Λε Κορμπυζιέ χρησιμοποίησε ρητά τη χρυσή αναλογία στο Modulor σύστημα του για την κλίμακα της αρχιτεκτονικής αναλογίας. Είδε το σύστημα αυτό, ως συνέχεια της μακράς παράδοσης του Βιτρούβιου,του "Άνθρωπος του Βιτρούβιου" του Leonardo da Vinci, του έργο του Leon Battista Alberti, και των άλλων που χρησιμοποίησαν τις αναλογίες του ανθρώπινου σώματος για να βελτιώσουν την εμφάνιση και τη λειτουργία της αρχιτεκτονικής. Εκτός από τη χρυσή αναλογία, ο Λε Κορμπυζιέ θεμελίωσε το σύστημα πάνω στις ανθρώπινες μετρήσεις και τους αριθμούς Φιμπονάτσι . Επίσης, πρότεινε την εφαρμογή της χρυσής αναλογίας σε ανθρώπινες αναλογίες: χώρισε το ύψος ενός ανθρώπινου μοντέλου στον ομφαλό με τα δύο τμήματα να βρίσκονται σε χρυσή αναλογία, κατόπιν υποδιαίρεσε αυτά τα δύο τμήματα σε χρυσή αναλογία στα γόνατα και το λαιμό και χρησιμοποίησε αυτές τις αναλογίες στο Modulor σύστημα του. Η Villa Stein στις Garches που σχεδίασε ο Λε Κορμπυζιέ το 1927 αποτέλεσε παράδειγμα της εφαρμογής του συστήματος του Modulor. Η ορθογώνια κάτοψη της βίλας, το υψόμετρο, και η εσωτερική δομή προσεγγίζονται από ορθογώνια με χρυσές αναλογίες.[13]
Ένας άλλος Ελβετός αρχιτέκτονας, ο Μάριο Μπότα (Mario Botta), βασίζει πολλά από τα σχέδιά του σε γεωμετρικά σχήματα. Αρκετές ιδιωτικές κατοικίες που σχεδίασε στην Ελβετία αποτελούνται από τετράγωνα και κύκλους, κύβους και κυλίνδρους. Σε ένα σπίτι που σχεδίασε στο Origlio, η χρυσή αναλογία είναι η αναλογία μεταξύ του κεντρικού τμήματος και των πλευρικών τμημάτων του σπιτιού.[14]
Σε ένα πρόσφατο βιβλίο, ο συγγραφέας Jason Elliot εικάζει ότι η χρυσή αναλογία χρησιμοποιήθηκε από τους σχεδιαστές του Naqsh-e Jahan Square και του παρακείμενου Lotfollah τζαμιού .[15]
Ζωγραφική
Η σχεδίαση του σώματος ενός άνδρα σε ένα πεντάγραμμο δείχνει τη σχέση με τη χρυσή αναλογία[16]
Ο φιλόσοφος Χάινριχ Κορνέλιους Αγκρίπα του 16ου αιώνα ζωγράφισε έναν άνθρωπο πάνω σ'ένα πεντάγραμμο μέσα σε ένα κύκλο, γεγονός που συνεπάγεται μια σχέση με τη χρυσή αναλογία.[16] Οι εικονογραφήσεις του Λεονάρντο ντα Βίντσι στα πολύεδρα στην De divina proportione (Στην θεϊκή αναλογία) και οι απόψεις του ότι ορισμένες σωματικές αναλογίες εμφανίζουν την χρυσή αναλογία έχουν οδηγήσει ορισμένους επιστήμονες να εικάζουν ότι ενσωμάτωσε τη χρυσή αναλογία στα έργα του.[17] Ωστόσο, η άποψη ότι στην Μόνα Λίζα , για παράδειγμα, χρησιμοποιεί χρυσή αναλογία, δεν υποστηρίζεται σε κανένα από τα κείμενα του.[18] Ομοίως, αν και ο Άνθρωπος του Βιτρούβιου συχνά [19] φαίνεται να είναι συνδεδεμένος με τη χρυσή αναλογία, οι αναλογίες του σχήματος στην πραγματικότητα δεν ταιριάζουν με αυτήν την άποψη, και το κείμενο αναφέρει μόνο αναλογίες ακεραίων αριθμών.[20]
Ο Σαλβαδόρ Νταλί, επηρεασμένος από τα έργα του Matila Ghyka,[21] χρησιμοποίησε ρητά τη χρυσή αναλογία στο αριστούργημά του,The Sacrament of the Last Supper (Το Μυστήριο του Μυστικού Δείπνου). Οι διαστάσεις του καμβά είναι ένα χρυσό ορθογώνιο. Ένα τεράστιο δωδεκάεδρο, με την προοπτική τα άκρα να εμφανίζονται σε χρυσή αναλογία μεταξύ τους, αναστέλλεται πάνω και πίσω από τον Ιησού.[22]
Έχει ειπωθεί ότι ο Πητ Μοντριάν έχει χρησιμοποιήσει την χρυσή τομή εκτενώς στα γεωμετρικά έργα του,[23] αν και άλλοι εμπειρογνώμονες (συμπεριλαμβανομένων του κριτικού Yve-Alain Bois) έχουν αμφισβητήσει τον ισχυρισμό αυτό.[6]
Σε μια στατιστική μελέτη σε 565 έργα τέχνης διαφόρων σπουδαίων ζωγράφων, η οποία διενεργήθηκε το 1999, διαπιστώθηκε ότι αυτοί οι καλλιτέχνες δεν είχαν χρησιμοποιήσει τη χρυσή αναλογία ως προς το μέγεθος των καμβάδων τους. Η μελέτη κατέληξε στο συμπέρασμα ότι η μέση αναλογία των δύο πλευρών των έργων ζωγραφικής είναι 1,34, με το μέσο όρο για μεμονωμένους καλλιτέχνες να κυμαίνεται από 1,04 (Γκόγια) σε 1,46 (Μπελλίνι).[24]
Μουσική
Ο Ernő Lendvai αναλύει τα έργα του Μπέλα Μπάρτοκ σαν να είναι βασισμένα σε δύο αντιτιθέμενα συστήματα,της χρυσής αναλογίας και της ακουστικής κλίμακας [25], αν και άλλοι επιστήμονες μουσικής απορρίπτουν την ανάλυση αυτή.[18] Στο Music for Strings,Percussion and Celesta του Bartok, η εξέλιξη του ξυλόφωνου συμβαίνει στα διαστήματα 1:2:3:5:8:5:3:2:1.[26] Ο Γάλλος συνθέτης Ερίκ Σατιέ χρησιμοποίησε τη χρυσή αναλογία σε πολλά από τα κομμάτια του, συμπεριλαμβανομένου του Sonneries de la Rose + Croix. Η χρυσή αναλογία είναι επίσης εμφανής στην οργάνωση των τμημάτων στη μουσική του Κλωντ Ντεμπυσσύ Reflets dans l'eau (Αντανακλάσεις στο νερό), από τις Εικόνες (1η σειρά, 1905), στις οποίες «η ακολουθία των πλήκτρων χαρακτηρίζεται από τα διαστήματα 34, 21, 13 και 8, και η κύρια κορύφωση εμφανίζεται στην θέση του φ ".[26]
Ο μουσικολόγος Roy Howat έχει παρατηρήσει ότι τα τυπικά όρια της La Mer αντιστοιχούν ακριβώς στη χρυσή τομή.[27] Ο Trezise βρίσκει τα εγγενή στοιχεία «αξιοσημείωτα», αλλά προειδοποιεί ότι κανένα γραπτό ή αναφερόμενο στοιχείο δεν δείχνει ότι ο Debussy αναζητούσε συνειδητά τέτοιες αναλογίες.[28]
Η εταιρία Pearl Drums τοποθετεί τους αεραγωγούς των Masters Premium μοντέλων της με βάση τη χρυσή αναλογία. Η εταιρεία ισχυρίζεται ότι η ρύθμιση αυτή βελτιώνει την απόκριση των μπάσων και έχει υποβάλει αίτηση για δίπλωμα ευρεσιτεχνίας για αυτή την καινοτομία.[29]
Φύση
Μία απεικόνιση της Aeonium tabuliforme στο Trädgårdsföreningen, Γκέτεμποργκ
Ο Adolf Zeising, του οποίου τα κύρια ενδιαφέροντα ήταν τα μαθηματικά και η φιλοσοφία, παρατήρησε τη χρυσή αναλογία να είναι εκφρασμένη στη διάταξη των κλαδιών,ανάμεσα στους μίσχους των φυτών και τις φλέβες στα φύλλα. Επέκτεινε την έρευνα του στους σκελετούς των ζώων και στις διακλαδώσεις των φλεβών και των νεύρων τους, με τις αναλογίες των χημικών ενώσεων και τη γεωμετρία των κρυστάλλων, ακόμη και με τη χρήση της αναλογίας σε καλλιτεχνικές προσπάθειες. Σε αυτά τα φαινόμενα είδε τη χρυσή αναλογία να λειτουργεί σαν καθολικός νόμος.[30] Σχετικά με το σχέδιό του για την χρυσή αναλογία με βάση τις ανθρώπινες αναλογίες του σώματος,ο Zeising έγραψε το 1854 για ένα καθολικό δίκαιο "στο οποίο περιέχεται το έδαφος-αρχή της όλης προσπάθειας για την ομορφιά και την πληρότητα στην σφαίρα τόσο της φύσης όσο και της τέχνης, και το οποίο διαπερνά, ως υψίστης σημασίας πνευματικό ιδεώδες, όλες τις δομές, μορφές και αναλογίες, είτε κοσμικές είτε μεμονωμένες, οργανικές ή ανόργανες, ηχητικές ή οπτικές.Και το οποίο βρίσκει την πληρέστερη υλοποίηση, ωστόσο, στην ανθρώπινη μορφή ".[31]
Το 2010, το περιοδικό Science ανέφερε ότι η χρυσή αναλογία είναι παρούσα σε ατομική κλίμακα στο μαγνητικό συντονισμό των περιστροφών στους κρυστάλλους κοβαλτίου νιοβίου.[32]
Αρκετοί ερευνητές έχουν προτείνει συνδέσεις μεταξύ της χρυσής αναλογίας και του ανθρώπινου DNA.[33][34][35]
Ωστόσο, ορισμένοι ερευνητές υποστηρίζουν ότι πολλές από τις εμφανείς περιπτώσεις της χρυσής τομής στη φύση, ιδίως σε σχέση με τις διαστάσεις των ζώων, στην πραγματικότητα είναι φανταστικές.[36]
Μαθηματικά
Συζυγής της Χρυσής Τομής
Η αρνητική ρίζα της δευτεροβάθμιας εξίσωσης του "φ" (η συζυγής ρίζα) είναι
-\frac{1}{\varphi}=1-\varphi = \frac{1 - \sqrt{5}}{2} = -0.61803\,39887\dots.
Η απόλυτη τιμή της ποσότητας αυτής (≈ 0.618) αντιστοιχεί στον αντίστροφο του λόγου του μήκους (μικρότερη πλευρά προς την μεγαλύτερη, b/a) και αναφέρεται μερικές φορές ως "συζυγής της χρυσής τομής".[37] Εδώ συμβολίζεται με το κεφαλαίο (Φ):
\Phi = {1 \over \varphi} = \varphi^{-1} = 0.61803\,39887\ldots.
Εναλλακτικά, το Φ μπορεί να εκφραστεί ως
\Phi = \varphi -1 = 1.61803\,39887\ldots -1 = 0.61803\,39887\ldots.
Αυτό καταδεικνύει την μοναδική ιδιότητα της χρυσής τομής ανάμεσα στους θετικούς αριθμούς,
{1 \over \varphi} = \varphi - 1,
ή την αντίστροφή της:
{1 \over \Phi} = \Phi + 1.
Αυτό σημαίνει ότι 0.61803...:1 = 1:1.61803....
Σύντομες αποδείξεις ότι o "φ" είναι άρρητος
Αντίφαση από μια έκφραση του ως ανάγωγο κλάσμα
Αν το φ ήταν ρητός, τότε θα ήταν ο λόγος πλευρών ενός ορθογωνίου παραλληλογράμμου με πλευρές ακεραίους. Αλλά είναι επίσης ο λόγος των πλευρών, οι οποίες είναι επίσης ακέραιοι, του μικρότερου ορθογωνίου παραλληλογράμμου που θα προκύψει αν αφαιρέσουμε από το αρχικό σχήμα ένα τετράγωνο. Η φθίνουσα ακολουθία των ακεραίων που σχηματίζεται από την συνεχή αφαίρεση τετραγώνων, δεν μπορεί να συνεχίζεται επ άπειρον, και έτσι το φ δεν μπορεί να είναι ρητός.
Ας θυμηθούμε ότι:
το όλο είναι το μεγαλύτερο τμήμα συν το μικρότερο
το όλο είναι για το μεγαλύτερο τμήμα ότι το μεγαλύτερο για το μικρότερο
Αν ονομάσουμε το όλο "n" και το μεγαλύτερο κομμάτι "m", τότε η δεύτερη πρόταση που ανακαλέσαμε γίνεται
το n είναι για το m ότι το m είναι για το n − m,
ή, αλγεβρικά εκφρασμένο
\frac nm = \frac{m}{n-m}.\qquad (*)
Το να είναι ο "φ" ρητός αριθμός σημαίνει ότι μπορεί να γραφεί ως κλάσμα n/m όπου τα μέλη του "n" και "m" είναι ακέραιοι. Μπορούμε χωρίς περιορισμό της γενικότητας να υποθέσουμε ότι το κλάσμα αυτό είναι ανάγωγο και ότι οι "n" και "m" είναι θετικοί. Αλλά αν συμβαίνει αυτό τότε, η παραπάνω ταυτότητα (*) λέει ότι το m/(n − m) έχει ακόμα μικρότερα μέλη από το n/m πράγμα άτοπο αφού υποθέσαμε ότι το n/m είναι ανάγωγο. Το άτοπο αυτό προέκυψε επειδή υποθέσαμε ότι ο "φ" είναι ρητός.
Πόρισμα του ότι ο √5 είναι άρρητος
Άλλη μια σύντομη απόδειξη—ίσως πιο διαδεδομένη—του ότι η χρυσή τομή είναι άρρητος αριθμός, είναι αυτή που χρησιμοποιεί το ότι το σύνολο των ρητών είναι "κλειστό" ως προς την συνήθη πρόσθεση και τον συνήθη πολλαπλασιασμό (το γινόμενο ρητών είναι ρητός και το άθροισμα των ρητών επίσης). Αν ο \textstyle\frac{1 + \sqrt{5}}{2} είναι ρητός, τότε και ο \textstyle2\left(\frac{1 + \sqrt{5}}{2} - \frac{1}{2}\right) = \sqrt{5} είναι επίσης ρητός, το οποίο όμως είναι αντίθετο με το γεγονός ότι ξέρουμε πως η τετραγωνική ρίζα όλων των μη-τετράγωνων φυσικών είναι άρρητος.
Άλλες μορφές
Προσσεγγίσεις του αντιστρόφου της χρυσής τομής από πεπερασμένα συνεχή κλάσματα, ή λόγους λόγους αριθμών Φιμπονάτσι
Η σχέση φ = 1 + 1/φ μπορεί να επεκταθεί αναδρομικά για να προκύψει ένα συνεχές κλάσμα για τη χρυσή τομή:[38]
\varphi = [1; 1, 1, 1, \dots] = 1 + \cfrac{1}{1 + \cfrac{1}{1 + \cfrac{1}{1 + \ddots}}}
και του αντιστρόφου της:
\varphi^{-1} = [0; 1, 1, 1, \dots] = 0 + \cfrac{1}{1 + \cfrac{1}{1 + \cfrac{1}{1 + \ddots}}}
Η εξίσωση φ2 = 1 + φ όμοια παράγει την μορφή συνεχής τετραγωνικής ρίζας:
\varphi = \sqrt{1 + \sqrt{1 + \sqrt{1 + \sqrt{1 + \cdots}}}}.
Μια άπειρη σειρά μπορεί να περιγράψει το φ:[39]
\varphi=\frac{13}{8}+\sum_{n=0}^{\infty}\frac{(-1)^{(n+1)}(2n+1)!}{(n+2)!n!4^{(2n+3)}}.
Ακόμα:
\varphi = 1+2\sin(\pi/10) = 1 + 2\sin 18^\circ
\varphi = {1 \over 2}\csc(\pi/10) = {1 \over 2}\csc 18^\circ
\varphi = 2\cos(\pi/5)=2\cos 36^\circ
\varphi = 2\sin(3\pi/10)=2\sin 54^\circ.
Αυτά αντιστοιχούν στο γεγονός ότι το μήκος της διαγωνίου ενός κανονικού πενταγώνου είναι "φ" φορές το μήκος της πλευράς του, και παρόμοιες σχέσεις σε ένα πεντάπλευρο.
Σχέση με την ακολουθία Fibonacci
Τα μαθηματικά της χρυσής αναλογίας και της ακολουθίας Fibonacci είναι στενά συνδεδεμένα μεταξύ τους. Η ακολουθία Fibonacci είναι:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, ....
Η κλειστής μορφής έκφραση για την ακολουθία Fibonacci(γνωστή ως φόρμουλα του Binet, μολονότι ήταν ήδη γνωστή από τον Abraham de Moivre περιλαμβάνει τη χρυσή αναλογία:
F\left(n\right) = {{\varphi^n-(1-\varphi)^n} \over {\sqrt 5}} = {{\varphi^n-(-\varphi)^{-n}} \over {\sqrt 5}}.
Μια σπείρα Fibonacci η οποία προσεγγίζει τη χρυσή σπείρα, χρησιμοποιώντας μεγέθη της ακολουθίας Fibonacci έως το 34.
Η χρυσή αναλογία είναι το όριο των λόγων των διαδοχικών όρων της ακολουθίας Fibonacci (ή οποιασδήποτε σαν την Fibonacci ακολουθία), όπως είχε αρχικά δείξει ο Kepler:[3]
\lim_{n\to\infty}\frac{F(n+1)}{F(n)}=\varphi.
Ως εκ τούτου, εάν ένας αριθμός Fibonacci διαιρείται με τον αμέσως προηγούμενο του στην ακολουθία, το πηλίκο προσεγγίζει το φ. Π.χ. 987/610 ≈ 1.6180327868852. Αυτές οι προσεγγίσεις είναι εναλλάξ χαμηλότερες και υψηλότερες από φ, και συγκλίνουν στο φ καθώς η ακολουθία Fibonacci είναι αύξουσα, και:
\sum_{n=1}^{\infty}|F(n)\varphi-F(n+1)| = \varphi.
Γενικότερα:
\lim_{n\to\infty}\frac{F(n+a)}{F(n)}={\varphi}^a,
όπου παραπάνω,οι αναλογίες των διαδοχικών όρων της ακολουθίας Fibonacci, είναι η περίπτωση όταν a = 1.
Επιπλέον, οι διαδοχικές δυνάμεις του φ υπακούν στην αναδρομική σχέση Fibonacci:
\varphi^{n+1} = \varphi^n + \varphi^{n-1}.
Αυτή η ταυτότητα επιτρέπει κάθε πολυώνυμο του φ να μειωθεί σε μία γραμμική έκφραση. Για παράδειγμα:
\begin{align} 3\varphi^3 - 5\varphi^2 + 4 & = 3(\varphi^2 + \varphi) - 5\varphi^2 + 4 \\ & = 3[(\varphi + 1) + \varphi] - 5(\varphi + 1) + 4 \\ & = \varphi + 2 \approx 3.618. \end{align}
Ωστόσο, αυτό δεν είναι κάποια ιδιαίτερη ιδιότητα του φ, διότι πολυώνυμα με λύση x σε μια δευτεροβάθμια εξίσωση μπορούν να μειωθούν κατά ανάλογο τρόπο, εφαρμόζοντας:
x^2=ax+b
για δεδομένους συντελεστές a, b τέτοιους ώστε το x να ικανοποιεί την εξίσωση.Πιο γενικά, οποιαδήποτε ρητή συνάρτηση (με ρητούς συντελεστές) της ρίζας ενός ανάγωγο πολυώνυμο n-οστού βαθμού μπορεί να μειωθεί σε ένα πολυώνυμο βαθμού n - 1. Διατυπώνοντας το από την πλευρά των σωμάτων, εάν α είναι η ρίζα ενός ανάγωγο πολυώνυμο n-οστού βαθμού,τότε το \Q(\alpha) έχει βαθμό n στο \Q, με βάση \{1, \alpha, \dots, \alpha^{n-1}\} .
Συμμετρίες
Η χρυσή αναλογία και το αντίστροφο της χρυσής αναλογίας \( \varphi_\pm = (1\pm \sqrt{5})/2 έχουν μια σειρά από συμμετρίες που διατηρούν και διαπλέκουν αυτές τις αναλογίες. Και οι δύο διατηρούνται από τις κλασματικές γραμμικές συναρτήσεις x, 1/(1-x), (x-1)/x,- το γεγονός αυτό αντιστοιχεί στην ταυτότητα και τον ορισμό της δευτεροβάθμιας εξίσωσης. Περαιτέρω, εναλλάσσονται με τις : 1/x, 1-x, x/(x-1)- που είναι αντίστροφες, συμμετρικές στο 1/2, και (προβολικά) συμμετρικές στο 2.
Αναλύοντας βαθύτερα, αυτές οι συναρτήσεις σχηματίζουν μια υποομάδα της ομάδας πηλίκο \operatorname{PSL}(2,\mathbf{Z}) ισόμορφη με την συμμετρική ομάδα S_3 , που αντιστοιχεί στον σταθεροποιητή του συνόλου \{0,1,\infty\} των 3 βασικών σημείων της προβολικής ευθείας, και οι συμμετρίες αντιστοιχούν στην ομάδα πηλίκο \( S_3 \to S_2 -η υποομάδα C_3 < S_3 - αποτελείται από το 3-κύκλους και η ταυτότητα () (0 1 \infty) (0 \infty 1) καθορίζει τους δύο αριθμούς, ενώ οι 2 κύκλοι εναλλάσσουν αυτούς, υλοποιώντας έτσι το χάρτη.
Άλλες αναλογίες
Η χρυσή αναλογία έχει την απλούστερη έκφραση(και την αργότερη σύγκλιση) ως συνεχιζόμενη επέκταση κλάσματος ενός αρρήτου αριθμού.Γι'αυτό το λόγο είναι μία από τις χειρότερες περιπτώσεις του θεωρήματος προσέγγισης του Lagrange και μία ακραία περίπτωση της ανισότητας του Hurwitz για τις διοφαντικές προσεγγίσεις.Αυτό μπορεί να εξηγεί γιατί γωνίες κοντά στην χρυσή αναλογία συχνά φαίνονται να είναι σε φυλλοταξία.[40]
Το ορισμένο πολυώνυμο δευτέρου βαθμού και η συζυγής σχέση αυτού οδηγούν σε δεκαδικές τιμές, οι οποίες έχουν το κλασματικό τους μέρος ίδιο με το κλασματικό μέρος του φ:
\varphi^2 = \varphi + 1 = 2.618\dots
{1 \over \varphi} = \varphi - 1 = 0.618\dots.
Η ακολουθία των δυνάμεων του φ περιλαμβάνει τις τιμές 0.618..., 1.0, 1.618..., 2.618....Γενικότερα,οποιαδήποτε δύναμη του φ είναι ίση με το άθροισμα των δυο αμέσως προηγούμενων δυνάμεων:
\varphi^n = \varphi^{n-1} + \varphi^{n-2} = \varphi \cdot \operatorname{F}_n + \operatorname{F}_{n-1}.
Ως αποτέλεσμα αυτού,εύκολα μπορούμε να διασπάσουμε μία δύναμη του φ σε μία πολλαπλή δύναμη του φ και μία σταθερά. Η πολλαπλή δύναμη του φ και η σταθερά είναι πάντα παρακείμενες της ακολουθίας Fibonacci.Αυτό οδηγεί σ' έναν άλλο λόγο των θετικών δυνάμεων του φ:
Αν \lfloor n/2 - 1 \rfloor = m ,τότε:
\!\ \varphi^n = \varphi^{n-1} + \varphi^{n-3} + \cdots + \varphi^{n-1-2m} + \varphi^{n-2-2m} \( \!\ \varphi^n - \varphi^{n-1} = \varphi^{n-2} .
Όταν η χρυσή αναλογία χρησιμοποιείται ως η βάση ενός αριθμητικού συστήματος,κάθε ακέραιος έχει μια τερματιζόμενη παράσταση,παρ'ότι ο φ είναι άρρητος,ενώ κάθε κλάσμα έχει μία μη-τερματιζόμενη παράσταση.
Η χρυσή αναλογία είναι θεμελιώδους σημασίας για το σώμα αριθμών \mathbb{Q}(\sqrt{5}) .Στο σώμα \mathbb{Q}(\sqrt{5}) έχουμε \varphi^n = {{L_n + F_n \sqrt{5}} \over 2} , όπου L_n είναι ο n-οστός όρος της Lucas ακολουθίας.
Η χρυσή αναλογία επίσης εμφανίζεται στην υπερβολική γεωμετρία ,ως η μέγιστη απόσταση ενός σημείου ενός ιδανικού τριγώνου με το κοντινότερο των άλλων δύο πλευρών: η απόσταση αυτή,το μήκος της πλευράς ενός ισοπλεύρου τριγώνου που σχηματίζεται από τα σημεία όπου εφάπτεται ένας κύκλος εγγεγραμμένος στο ιδανικό τρίγωνο,είναι 4 ln φ.[41]
Δεκαδική επέκταση
Η δεκαδική επέκταση της χρυσής αναλογίας μπορεί να υπολογιστεί κατευθείαν από το τύπο
\varphi = {1+\sqrt{5} \over 2}
με √5 ≈ 2.2360679774997896964 .Η τετραγωνική ρίζα του 5 μπορεί να υπολογιστεί με την Βαβυλώνια μέθοδο,ξεκινώντας με αρχική εκτίμηση όπως xφ = 2 και συνεχίζοντας με την επαναληπτική σχέση
x_{n+1} = \frac{(x_n + 5/x_n)}{2}
για n = 1, 2, 3, ...,μέχρι η διαφορά μεταξύ του xn και του xn−1 να γίνει 0,στον επιθυμητό αριθμό ψηφίων.
Ο Βαβυλώνιος αλγόριθμος για √5 είναι ισοδύναμος με την μέθοδο του Newton για την επίλυση της εξίσωσης x2 − 5 = 0 .Στην πιο γενική μορφή της,η μέθοδος του Newton μπορεί να εφαρμοστεί κατευθείαν σε οποιαδήποτε αλγεβρική εξίσωση ,συμπεριλαμβανομένης της εξίσωσης x2 − x − 1 = 0 η οποία ορίζει την χρυσή αναλογία.Αυτή δίνει μία επαναληπτική σχέση που συγκλίνει στην χρυσή αναλογία από μόνη της,
x_{n+1} = \frac{x_n^2 + 1}{2x_n - 1},
για μία κατάλληλη αρχική εκτίμηση xφ όπως xφ = 1.Μία ελαφρώς γρηγορότερη μέθοδος είναι να ξαναγράψουμε την εξίσωση ως x − 1 − 1/x = 0 ,στην οποία περίπτωση η επαναληπτική σχέση του Newton γίνεται
x_{n+1} = \frac{x_n^2 + 2x_n}{x_n^2 + 1}.
Αυτές οι επαναλήψεις συγκλίνουν όλες τετραγωνικά.Δηλαδή ,κάθε βήμα διπλασιάζει περίπου τον αριθμό των σωστών ψηφίων.Η χρυσή αναλογία είναι επομένως σχετικά εύκολο να υπολογιστεί με ακρίβεια.Ο χρόνος που χρειάζεται για να υπολογίσουμε n ψηφία της χρυσής αναλογίας είναι ανάλογος του χρόνου που χρειάζεται για να διαιρέσουμε δύο αριθμούς με n ψηφία.Αυτό είναι πολύ γρηγορότερο από γνωστούς αλγόριθμους για τους αριθμούς π και e.
Μία εύκολη εναλλακτική λύση χρησιμοποιώντας μόνο ακέραιη αριθμητική είναι να υπολογίσουμε δύο μεγάλες διαδοχικές ακολουθίες Fibonacci και να τις διαιρέσουμε.Η αναλογία των αριθμών Fibonacci F 25001 και F 25000,ο καθένας πάνω από 5.000 ψηφία,αποδίδει πάνω από 10.000 σημαντικά ψηφία της χρυσής αναλογίας.
Η χρυσή αναλογία φ έχει υπολογιστεί με ακρίβεια πολλών χιλιάδων δεκαδικών ψηφίων.Ο Alexis Irlande εκτέλεσε υπολογισμούς και την επαλήθευση των πρώτων 17 δισεκατομμυρίων ψηφίων.[42]
Πυραμίδες
Μια κανονική πυραμίδα με βάση τετράγωνο καθορίζεται από ένα εσωτερικό ορθογώνιο τρίγωνο,του οποίου οι πλευρές είναι το απόστημα της πυραμίδας (α),η ημι-βάση της (b) και το ύψος της (h). Η κλίση της γωνίας σημειώνεται επίσης. Μαθηματικές αναλογίες b: h: α όπως 1:\sqrt{\varphi}:\varphi και 3:4:5\ και 1:4/\pi:1.61899\ παρουσιάζουν ιδιαίτερο ενδιαφέρον σε σχέση με τις πυραμίδες της Αιγύπτου.
Οι πυραμίδες της Αιγύπτου καθώς και οι μαθηματικές κανονικές πυραμίδες που μοιάζουν με αυτές μπορούν να αναλυθούν σε σχέση με την χρυσή και τις άλλες αναλογίες.
Μαθηματικές πυραμίδες και τρίγωνα
Μια πυραμίδα στην οποία το απόστημα (ύψος της παράπλευρης έδρας ) είναι ίσο με φ φορές την ημι-βάση (το ήμισυ του πλάτους βάσης) ονομάζεται μερικές φορές χρυσή πυραμίδα. Το ισοσκελές τρίγωνο, που είναι το πρόσωπο μιας τέτοιας πυραμίδας μπορεί να κατασκευαστεί από τα δύο μισά ενός ορθογώνιου με χρυσές αναλογίες,ενώνοντας τις μεσαίου μήκους πλευρές για να κάνουν το απόστημα. Το ύψος αυτής της πυραμίδας είναι \sqrt{\varphi} φορές την ημι-βάση και το τετράγωνο του ύψους είναι ίσο με την πλευρά της πυραμίδας,δηλαδή φ φορές το τετράγωνο της ημι-βάσης.
Το μεσαίο ορθογώνιο τρίγωνο αυτής της "χρυσής" πυραμίδας (βλέπε διάγραμμα), με πλευρές 1:\sqrt{\varphi}:\varphi είναι ενδιαφέρον από μόνο του, αποδεικνύοντας με το Πυθαγόρειο θεώρημα τη σχέση \sqrt{\varphi} = \sqrt{\varphi^2 - 1} ή \varphi = \sqrt{1 + \varphi} . Αυτό το "Τρίγωνο του Κέπλερ" [43] είναι η μόνη αναλογία ορθογώνιου τριγώνου με μήκη πλευρών σε γεωμετρική πρόοδο,[44] όπως ακριβώς το 3-4-5 τρίγωνο είναι η μόνη αναλογία ορθογώνιου τριγώνου με μήκη πλευρών σε αριθμητική πρόοδο. Η γωνία με εφαπτομένη \sqrt{\varphi} αντιστοιχεί στη γωνία που σχηματίζεται από την πλευρά της πυραμίδας και το έδαφος, 51,827 ... μοίρες (51 ° 49 '38 ").[45]
Ένα σχεδόν παρόμοιο σχήμα πυραμίδας, αλλά με ρητές αναλογίες, περιγράφεται στο Rhind Mathematical Papyrus (την πηγή ενός μεγάλου μέρους της σύγχρονης γνώσης των αρχαίων αιγυπτιακών μαθηματικών),βασισμένο στο τρίγωνο 3:4:5.[46] Η κλίση της πυραμίδας που αντιστοιχεί στη γωνία με εφαπτομένη 4/3 είναι 53,13 μοίρες (53 μοίρες και 8 λεπτά).[47] Το απόστημα ή το ύψος της παράπλευρης έδρας είναι 5/3 ή 1.666 ... φορές την ημι-βάση.Το Rhind Papyrus έχει ακόμη ένα πρόβλημα με την πυραμίδα, πάλι με την κλίση ρητών αριθμών. Τα αιγυπτιακά μαθηματικά δεν περιλαμβάνουν την έννοια των άρρητων αριθμών,[48] και η αντίστροφη κλίση ρητών αριθμών χρησιμοποιήθηκε στην κατασκευή των πυραμίδων.[46]
Μια άλλη μαθηματική πυραμίδα με αναλογίες σχεδόν ταυτόσημες με της «χρυσής» είναι αυτή με περίμετρο ίση με 2π φορές το ύψος της, ή h: b = 4: π. Αυτό το τρίγωνο έχει μια γωνία κλίσης 51.854 ° (51 ° 51 '), πολύ κοντά στις ° 51.827 του τριγώνου του Kepler. Αυτή η σχέση της πυραμίδα αντιστοιχεί στην σχέση \ sqrt{\varphi} \approx 4/\pi.
Αιγυπτιακές πυραμίδες
Στα μέσα του δέκατου ένατου αιώνα,ο Röber μελέτησε ποικίλες Αιγυπτιακές πυραμίδες συμπεριλαμβανομένων των Khafre, Menkaure και μερικών από της Γκίζας και Σαxάρας και ερμηνεύτηκε ότι είπε ότι το μισό της βάσης της πυραμίδας είναι η μέση της πλευράς ,διατυπώνοντας ότι οι άλλοι συγγραφείς αναγνώριζαν ως το τρίγωνο του Kepler. Πολλές άλλες μαθηματικές θεωρίες σε σχέση με το σχήμα των πυραμίδων έχουν επίσης διερευνηθεί.[44]
Μία Αιγυπτιακή πυραμίδα εξαιρετικά κοντά σε μια "χρυσή πυραμίδα" είναι η Μεγάλη Πυραμίδα της Γκίζας (επίσης γνωστή ως η Πυραμίδα του Χέοπα). Η κλίση της 51 ° 52 'είναι πολύ κοντά στην "χρυσή" κλίση της πυραμίδας των 51 ° 50' και στην βασισμένη στον αριθμό π κλίση της πυραμίδας των 51 ° 51 '. Άλλες πυραμίδες της Γκίζας (Chephren, 52 ° 20', και Mycerinus, 50 ° 47 '),[46] είναι επίσης αρκετά κοντά. Το αν η σχέση με τη χρυσή αναλογία σε αυτές τις πυραμίδες έχει σχεδιαστεί ή έχει προκύψει κατά λάθος παραμένει άγνωστο.[49] Επίσης,αρκετές άλλες Αιγυπτιακές πυραμίδες είναι πολύ κοντά στο 3:4:5 σχήμα.[47]
Συμβάλλοντας έντονα στην αντιπαράθεση ο αρχιτεκτονικός συντάκτης της Μεγάλης Πυραμίδας,Eric Temple Bell, μαθηματικός και ιστορικός, ισχυρίστηκε το 1950 ότι τα Αιγυπτιακά μαθηματικά δεν θα είχαν την δυνατότητα να υπολογίσουν το ύψος της παράπλευρης έδρας της πυραμίδας, ή την αναλογία προς το ύψος, εκτός από την περίπτωση της 3:4:5 πυραμίδας,δεδομένου ότι το τρίγωνο 3:4:5 ήταν το μόνο ορθογώνιο τρίγωνο γνωστό στους Αιγυπτίους. Επιπλέον,υποστήριξε ότι οι αρχαίοι Αιγύπτιοι δεν γνώριζαν το Πυθαγόρειο θεώρημα και με κανέναν τρόπο δεν θα μπορούσαν να εξηγήσουν άρρητους αριθμούς, όπως ο π ή ο φ.[50]
Ο Michael Rice [51] ισχυρίζεται ότι οι κύριες αρχές στην ιστορία της αιγυπτιακής αρχιτεκτονικής έχουν υποστηρίξει ότι οι Αιγύπτιοι ήταν εξοικειωμένοι με τη χρυσή αναλογία ,η οποία αποτελεί κομμάτι των μαθηματικών των πυραμίδων, όπως αναφέρει ο Giedon (1957).[52] Οι ιστορικοί των επιστημών ανέκαθεν διαφωνούσαν για το αν οι Αιγύπτιοι είχαν κάποια τέτοια γνώση ή όχι, αντιτάσσοντας ότι η εμφάνιση της χρυσής τομής στις πυραμίδες ήταν προιον τύχης.[53]
Το 1859, ο πυραμιδιολόγος John Taylor ισχυρίστηκε ότι, στη Μεγάλη Πυραμίδα της Γκίζας, η χρυσή αναλογία εκπροσωπείται από την αναλογία του ύψους της παράπλευρης έδρας,σχηματίζοντας μια γωνία θ με το έδαφος, προς το μισό του μήκους της πλευράς της βάσης, που ισοδυναμεί με την τέμνουσα της γωνίας θ.[54] Τα παραπάνω δύο μήκη ήταν περίπου 186,4 και 115,2 μέτρα αντίστοιχα. Η αναλογία αυτών των μηκών είναι η χρυσή αναλογία, με ακρίβεια περισσοτέρων ψηφίων από αυτών στις αρχικές μετρήσεις. Ομοίως,ο Howard Vyse, σύμφωνα με το Matila Ghyka,[55] ανέφερε το ύψος της Μεγάλης πυραμίδας 148,2 m, και το μισό μήκος της πλευράς της βάσης της 116,4 m, αποδίδοντας 1,6189 για το λόγο του ύψους της παράπλευρης έδρας προς το μισό μήκος της πλευράς της βάσης, και πάλι με μεγαλύτερη ακρίβεια .
Επίμαχες παρατηρήσεις
Παραδείγματα επίμαχων παρατηρήσεων σε σχέση με την χρυσή τομή παραθέτονται παρακάτω:
Ο ιστορικός John Man αναφέρει ότι οι σελίδες της Βίβλου του Γουτεμβέργιου ήταν "βασισμένες στο σχήμα της χρυσή τομής". Ωστόσο, σύμφωνα με τις μετρήσεις του ίδιου, ο λόγος του ύψους προς το πλάτος ήταν 1,45.[56]
Ορισμένες συγκεκριμένες αναλογίες στα σώματα πολλών ζώων, στα σώματα των ανθρώπων[57][58],σε τμήματα των κελυφών των μαλακίων καθώς και στα κεφαλόποδα συχνά φέρονται να είναι στην χρυσή αναλογία. Υπάρχει μια μεγάλη διακύμανση των πραγματικών μετρήσεων των στοιχείων αυτών σε συγκεκριμένα άτομα, όμως, και η εν λόγω αναλογία είναι συχνά σημαντικά διαφορετική από την χρυσή αναλογία.[57] Η αναλογία των διαδοχικών φαλάγγιων οστών και του μετακαρπίου οστού λέγεται ότι προσεγγίζει τη χρυσή αναλογία.[58] Ο ναύτιλος, η κατασκευή του οποίου προχωρά σε μια λογαριθμική σπείρα, αναφέρεται συχνά, συνήθως με την άποψη ότι κάθε λογαριθμική σπείρα σχετίζεται με τη χρυσή αναλογία, αλλά μερικές φορές και με τον ισχυρισμό ότι κάθε νέα θάλαμος βρίσκεται σε χρυσή αναλογία με την προηγούμενη.[59] Ωστόσο, οι μετρήσεις των μαλακίων αυτών δεν υποστηρίζουν τον ισχυρισμό αυτό [60].
Οι αναλογίες των διαφόρων συστατικών των φυτών (αριθμοί των φύλλων στα κλαδιά, διάμετροι των γεωμετρικών σχημάτων μέσα σε λουλούδια) υποστηρίζεται ότι συχνά παρουσιάζουν την χρυσή αναλογία σε διάφορα είδη.[61] Στην πράξη, υπάρχουν σημαντικές διαφορές μεταξύ των ατόμων, εποχιακές διαφορές, και ηλικιακές διαφορές σε αυτά τα είδη.
Στον τομέα των επενδύσεων, ορισμένοι επαγγελματίες της τεχνικής ανάλυσης χρησιμοποιούν τη χρυσή αναλογία για να υποστηρίξουν ένα επίπεδο τιμών ή την αντίσταση τους στις αυξήσεις των τιμών, μιας μετοχής ή ενός εμπορεύματος. Μετά από σημαντικές μεταβολές των τιμών προς τα πάνω ή προς τα κάτω, νέα επίπεδα στήριξης και αντίστασης υποτίθεται ότι βρέθηκαν στις τιμές αυτές ή κοντά σε αυτές που συνδέονται με την τιμή εκκίνησης μέσω της χρυσής αναλογίας.[62] Η χρήση της χρυσής αναλογίας όσον αφορά στις επενδύσεις, σχετίζεται επίσης με πιο περίπλοκα σχέδια που περιγράφονται από τους αριθμούς Fibonacci. Ωστόσο, άλλοι αναλυτές της αγοράς έχουν δημοσιεύσει αναλύσεις που υποδηλώνουν ότι αυτά τα ποσοστά και τα πρότυπα δεν υποστηρίζονται από τα δεδομένα.[63]
Βιβλιογραφία
H. E. Huntley, The Divine Proportion: A Study in Mathematical Beauty, New York: 1970
Mario Livio, The Golden Ratio: The Story of PHI, the World's Most Astonishing Number, 2003
Hrant Arakelyan. Mathematics and History of the Golden Section. – Logos 2014, 404 p. —ISBN 978-5-98704-663-0, (rus.).
Παραπομπές
Hemenway, Priya (2005). Divine Proportion: Phi In Art, Nature, and Science. New York: Sterling, σελ. 20–21. ISBN 1-4027-3522-7.
Plato (360 BC) (Benjamin Jowett trans.). «Timaeus». The Internet Classics Archive. Ανακτήθηκε στις 2006-05-30.
James Joseph Tattersall (2005). Elementary number theory in nine chapters (2nd έκδοση). Cambridge University Press, σελ. 28. ISBN 978-0-521-85014-8.
Underwood Dudley (1999). Die Macht der Zahl: Was die Numerologie uns weismachen will. Springer, σελ. 245. ISBN 3-7643-5978-1.
Cook, Theodore Andrea (1979) [1914]. The Curves of Life. New York: Dover Publications. ISBN 0-486-23701-X.
^ a b c d e f g Livio, Mario (2002). The Golden Ratio: The Story of Phi, The World's Most Astonishing Number. New York: Broadway Books. ISBN 0-7679-0815-5.
Van Mersbergen, Audrey M., "Rhetorical Prototypes in Architecture: Measuring the Acropolis with a Philosophical Polemic", Communication Quarterly, Vol. 46 No. 2, 1998, pp 194-213.
Midhat J. Gazalé , Gnomon, Princeton University Press, 1999. ISBN 0-691-00514-1
Keith J. Devlin The Math Instinct: Why You're A Mathematical Genius (Along With Lobsters, Birds, Cats, And Dogs), p. 108. New York: Thunder's Mouth Press, 2005, ISBN 1-56025-672-9
Patrice Foutakis, Did the Greeks Build According to the Golden Ratio?, Cambridge Archaeological Journal, vol. 24, n° 1, February 2014, σελ. 71-86.
Boussora, Kenza and Mazouz, Said, The Use of the Golden Section in the Great Mosque of Kairouan, Nexus Network Journal, vol. 6 no. 1 (Spring 2004), [1]
Le Corbusier, The Modulor p. 25, as cited in Padovan, Richard, Proportion: Science, Philosophy, Architecture (1999), p. 316, Taylor and Francis, ISBN 0-419-22780-6
Le Corbusier, The Modulor, p. 35, as cited in Padovan, Richard, Proportion: Science, Philosophy, Architecture (1999), p. 320. Taylor & Francis. ISBN 0-419-22780-6: "Both the paintings and the architectural designs make use of the golden section".
Urwin, Simon. Analysing Architecture (2003) pp. 154-5, ISBN 0-415-30685-X
Jason Elliot (2006). Mirrors of the Unseen: Journeys in Iran. Macmillan, σελ. 277, 284. ISBN 978-0-312-30191-0.
Piotr Sadowski (1996). The knight on his quest: symbolic patterns of transition in Sir Gawain and the Green Knight. University of Delaware Press, σελ. 124. ISBN 978-0-87413-580-0.
Leonardo da Vinci's Polyhedra, by George W. Hart[2]
Livio, Mario. «The golden ratio and aesthetics». Ανακτήθηκε στις 2008-03-21.
"Part of the process of becoming a mathematics writer is, it appears, learning that you cannot refer to the golden ratio without following the first mention by a phrase that goes something like 'which the ancient Greeks and others believed to have divine and mystical properties.' Almost as compulsive is the urge to add a second factoid along the lines of 'Leonardo Da Vinci believed that the human form displays the golden ratio.' There is not a shred of evidence to back up either claim, and every reason to assume they are both false. Yet both claims, along with various others in a similar vein, live on." Keith Devlin (May 2007). «The Myth That Will Not Go Away». Αρχειοθετήθηκε από το πρωτότυπο στις May 23, 2007. Ανακτήθηκε στις April 10, 2013.
Donald E. Simanek. «Fibonacci Flim-Flam». Ανακτήθηκε στις April 9, 2013.
Σφάλμα στην κλήση του template:cite video: Οι παράμετροι publisher, time, url και title πρέπει να οριστούν. The Dali Dimension: Decoding the Mind of a Genius (English) Media 3.14-TVC-FGSD-IRL-AVRO (DVD) (2008)
Hunt, Carla Herndon and Gilkey, Susan Nicodemus. Teaching Mathematics in the Block pp. 44, 47, ISBN 1-883001-51-X
Bouleau, Charles, The Painter's Secret Geometry: A Study of Composition in Art (1963) pp.247-8, Harcourt, Brace & World, ISBN 0-87817-259-9
Olariu, Agata, Golden Section and the Art of Painting Available online
Lendvai, Ernő (1971). Béla Bartók: An Analysis of His Music. London: Kahn and Averill.
Smith, Peter F. The Dynamics of Delight: Architecture and Aesthetics (New York: Routledge, 2003) pp 83, ISBN 0-415-30010-X
Roy Howat (1983). Debussy in Proportion: A Musical Analysis. Cambridge University Press. ISBN 0-521-31145-4.
Simon Trezise (1994). Debussy: La Mer. Cambridge University Press, σελ. 53. ISBN 0-521-44656-2.
«Pearl Masters Premium». Pearl Corporation. Ανακτήθηκε στις December 2, 2007.[νεκρός σύνδεσμος]
Richard Padovan (1999). Proportion. Taylor & Francis, σελ. 305–306. ISBN 978-0-419-22780-9.
Zeising, Adolf, Neue Lehre van den Proportionen des meschlischen Körpers, Leipzig, 1854, preface.
«Golden ratio discovered in a quantum world». Eurekalert.org. 2010-01-07. Ανακτήθηκε στις 2011-10-31.
J.C. Perez (1991), "Chaos DNA and Neuro-computers: A Golden Link", in Speculations in Science and Technology vol. 14 no. 4, ISSN 0155-7785.
Yamagishi, Michel E.B., and Shimabukuro, Alex I. (2007), "Nucleotide Frequencies in Human Genome and Fibonacci Numbers", in Bulletin of Mathematical Biology, ISSN 0092-8240 (print), ISSN 1522-9602 (online). PDF full text
Perez, J.-C. (September 2010). «Codon populations in single-stranded whole human genome DNA are fractal and fine-tuned by the Golden Ratio 1.618». Interdisciplinary Sciences: Computational Life Science 2 (3): 228–240. doi:10.1007/s12539-010-0022-0. PMID 20658335.
Pommersheim, James E., Tim K. Marks, and Erica L. Flapan, eds. 2010. Number Theory: A lively Introduction with Proofes, Applications, and Stories. John Wiley and Sons: 82.
Weisstein, Eric W., "Golden Ratio Conjugate" από το MathWorld.
Max. Hailperin, Barbara K. Kaiser, and Karl W. Knight (1998). Concrete Abstractions: An Introduction to Computer Science Using Scheme. Brooks/Cole Pub. Co. ISBN 0-534-95211-9.
Brian Roselle, "Golden Mean Series"
Fibonacci Numbers and Nature - Part 2 : Why is the Golden section the "best" arrangement?, from Dr. Ron Knott's Fibonacci Numbers and the Golden Section, retrieved 2012-11-29.
Horocycles exinscrits : une propriété hyperbolique remarquable, cabri.net, retrieved 2009-07-21.
The golden number to 17 000 000 000 digits. Universidad Nacional de Colombia. 2008.[νεκρός σύνδεσμος]
Radio, Astraea Web (2006). The Best of Astraea: 17 Articles on Science, History and Philosophy. Astrea Web Radio. ISBN 1-4259-7040-0.
Roger Herz-Fischler (2000). The Shape of the Great Pyramid. Wilfrid Laurier University Press. ISBN 0-88920-324-5.
Midhat Gazale, Gnomon: From Pharaohs to Fractals, Princeton Univ. Press, 1999
Eli Maor, Trigonometric Delights, Princeton Univ. Press, 2000
«The Great Pyramid, The Great Discovery, and The Great Coincidence». Ανακτήθηκε στις 2007-11-25.[νεκρός σύνδεσμος]
Lancelot Hogben, Mathematics for the Million, London: Allen & Unwin, 1942, p. 63., as cited by Dick Teresi, Lost Discoveries: The Ancient Roots of Modern Science—from the Babylonians to the Maya, New York: Simon & Schuster, 2003, p.56
Burton, David M. (1999). The history of mathematics: an introduction (4 έκδοση). WCB McGraw-Hill, σελ. 56. ISBN 0-07-009468-3.
Eric Temple Bell, The Development of Mathematics, New York: Dover, 1940, p.40
Rice, Michael, Egypt's Legacy: The Archetypes of Western Civilisation, 3000 to 30 B.C pp. 24 Routledge, 2003, ISBN 0-415-26876-1
S. Giedon, 1957, The Beginnings of Architecture, The A.W. Mellon Lectures in the Fine Arts, 457, as cited in Rice, Michael, Egypt's Legacy: The Archetypes of Western Civilisation, 3000 to 30 B.C pp.24 Routledge, 2003
Markowsky, George (January 1992). «Misconceptions about the Golden Ratio» (PDF). College Mathematics Journal (Mathematical Association of America) 23 (1): 2–19. doi:10.2307/2686193.
Taylor, The Great Pyramid: Why Was It Built and Who Built It?, 1859
Matila Ghyka The Geometry of Art and Life, New York: Dover, 1977
Man, John, Gutenberg: How One Man Remade the World with Word (2002) pp. 166–167, Wiley, ISBN 0-471-21823-5. "The half-folio page (30.7 × 44.5 cm) was made up of two rectangles—the whole page and its text area—based on the so called 'golden section', which specifies a crucial relationship between short and long sides, and produces an irrational number, as pi is, but is a ratio of about 5:8."
Pheasant, Stephen (1998). Bodyspace. London: Taylor & Francis. ISBN 0-7484-0067-2.
van Laack, Walter (2001). A Better History Of Our World: Volume 1 The Universe. Aachen: van Laach GmbH.
Ivan Moscovich, Ivan Moscovich Mastermind Collection: The Hinged Square & Other Puzzles, New York: Sterling, 2004
Peterson, Ivars. «Sea shell spirals». Science News.
Derek Thomas, Architecture and the Urban Environment: A Vision for the New Age, Oxford: Elsevier, 2002
For instance, Osler writes that "38.2 percent and 61.8 percent retracements of recent rises or declines are common," in Osler, Carol (2000). «Support for Resistance: Technical Analysis and Intraday Exchange Rates» (PDF). Federal Reserve Bank of New York Economic Policy Review 6 (2): 53–68.
Roy Batchelor and Richard Ramyar, "Magic numbers in the Dow," 25th International Symposium on Forecasting, 2005, p. 13, 31. "Not since the 'big is beautiful' days have giants looked better", Tom Stevenson, The Daily Telegraph, Apr. 10, 2006, and "Technical failure", The Economist, Sep. 23, 2006, are both popular-press accounts of Batchelor and Ramyar's research.
Εξωτερικοί σύνδεσμοι
Ο χρυσός αριθμός - Φ - (από το www.asxetos.gr)
Η χρυσή τομή στην τέχνη και την αρχιτεκτονική (Αγγλικά)
Hellenica World - Scientific Library
Από τη ελληνική Βικιπαίδεια http://el.wikipedia.org . Όλα τα κείμενα είναι διαθέσιμα υπό την GNU Free Documentation License

