The truncated square antiprism one in an infinite series of truncated antiprisms, constructed as a truncated square antiprism. It has 18 faces, 2 octagons, 8 hexagons, and 8 squares.
Gyroelongated triamond square bicupola
If the hexagons are folded, it can be constructed by regular polygons. Or each folded hexagon can be replaced by two triamonds, adding 8 edges (56), and 4 faces (32). This form is called a gyroelongated triamond square bicupola.[1]
Related polyhedra
| Symmetry | D2d, [2+,4], (2*2) | D3d, [2+,6], (2*3) | D4d, [2+,8], (2*4) | D5d, [2+,10], (2*5) |
|---|---|---|---|---|
| Antiprisms |  s{2,4} (v:4; e:8; f:6) |
 s{2,6} (v:6; e:12; f:8) |
 s{2,8} (v:8; e:16; f:10) |
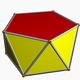 s{2,10} (v:10; e:20; f:12) |
| Truncated antiprisms |
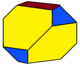 ts{2,4} (v:16;e:24;f:10) |
 ts{2,6} (v:24; e:36; f:14) |
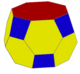 ts{2,8} (v:32; e:48; f:18) |
 ts{2,10} (v:40; e:60; f:22) |
Snub square antiprism
Although it can't be made by all regular planar faces, its alternation is the Johnson solid, the snub square antiprism.
Snub square antiprism colored.png
References
Convex Triamond Regular Polyhedra
Snub Anti-Prisms
Undergraduate Texts in Mathematics
Graduate Studies in Mathematics
Hellenica World - Scientific Library
Retrieved from "http://en.wikipedia.org/"
All text is available under the terms of the GNU Free Documentation License


