Truncated 120-cells

In geometry, a truncated 120-cell is a uniform 4-polytope formed as the truncation of the regular 120-cell.

There are three trunctions, including a bitruncation, and a tritruncation, which creates the truncated 600-cell.

Truncated 120-cell

Truncated 120-cell
Schlegel diagram (tetrahedron cells visible)
Type	Uniform 4-polytope
Uniform index	36
Schläfli symbol	t0,1{5,3,3} or t{5,3,3}
Coxeter diagrams
Cells	600 3.3.3 120 3.10.10
Faces	2400 triangles 720 decagons
Edges	4800
Vertices	2400
Vertex figure	triangular pyramid
Dual	Tetrakis 600-cell
Symmetry group	H4, [3,3,5], order 14400
Properties	convex

Net

The truncated 120-cell or truncated hecatonicosachoron is a uniform 4-polytope, constructed by a uniform truncation of the regular 120-cell 4-polytope.

It is made of 120 truncated dodecahedral and 600 tetrahedral cells. It has 3120 faces: 2400 being triangles and 720 being decagons. There are 4800 edges of two types: 3600 shared by three truncated dodecahedra and 1200 are shared by two truncated dodecahedra and one tetrahedron. Each vertex has 3 truncated dodecahedra and one tetrahedron around it. Its vertex figure is an equilateral triangular pyramid.
Alternate names

Truncated 120-cell (Norman W. Johnson)
Tuncated hecatonicosachoron / Truncated dodecacontachoron / Truncated polydodecahedron
Truncated-icosahedral hexacosihecatonicosachoron (Acronym thi) (George Olshevsky, and Jonathan Bowers)[1]

Images

Orthographic projections by Coxeter planes

H4	-	F4
[30]	[20]	[12]
H3	A2	A3
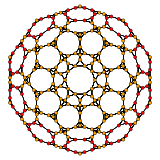[10]	[6]	[4]

Truncated 120-cell net.png
net Truncated 120cell.png
Central part of stereographic projection
(centered on truncated dodecahedron) Stereographic truncated 120-cell.png
Stereographic projection

120-cell	Truncated 120-cell	Rectified 120-cell	Bitruncated 120-cell Bitruncated 600-cell
600-cell	Truncated 600-cell	Rectified 600-cell
Orthogonal projections in H3 Coxeter plane

Bitruncated 120-cell

Bitruncated 120-cell
Schlegel diagram, centered on truncated icosahedron, truncated tetrahedral cells visible
Type	Uniform 4-polytope
Uniform index	39
Coxeter diagram
Schläfli symbol	t1,2{5,3,3} or 2t{5,3,3}
Cells	720: 120 5.6.6 600 3.6.6
Faces	4320: 1200{3}+720{5}+ 2400{6}
Edges	7200
Vertices	3600
Vertex figure	digonal disphenoid
Symmetry group	H4, [3,3,5], order 14400
Properties	convex, vertex-transitive

Net

The bitruncated 120-cell or hexacosihecatonicosachoron is a uniform 4-polytope. It has 720 cells: 120 truncated icosahedra, and 600 truncated tetrahedra. Its vertex figure is a digonal disphenoid, with two truncated icosahedra and two truncated tetrahedra around it.

Alternate names

Bitruncated 120-cell / Bitruncated 600-cell (Norman W. Johnson)
Bitruncated hecatonicosachoron / Bitruncated hexacosichoron / Bitruncated polydodecahedron / Bitruncated polytetrahedron
Truncated-icosahedral hexacosihecatonicosachoron (Acronym Xhi) (George Olshevsky, and Jonathan Bowers)[2]

Images

Stereographic projection (Close up)

Orthographic projections by Coxeter planes

H4	-	F4
[30]	[20]	[12]
H3	A2 / B3 / D4	A3 / B2
[10]	[6]	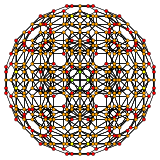[4]

Truncated 600-cell

Truncated 600-cell
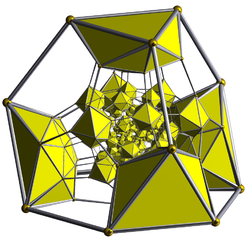Schlegel diagram (icosahedral cells visible)
Type	Uniform 4-polytope
Uniform index	41
Schläfli symbol	t0,1{3,3,5} or t{3,3,5}
Coxeter diagram
Cells	720: 120 3.3.3.3.3 600 3.6.6
Faces	2400{3}+1200{6}
Edges	4320
Vertices	1440
Vertex figure	pentagonal pyramid
Dual	Dodecakis 120-cell
Symmetry group	H4, [3,3,5], order 14400
Properties	convex

Net

The truncated 600-cell or truncated hexacosichoron is a uniform 4-polytope. It is derived from the 600-cell by truncation. It has 720 cells: 120 icosahedra and 600 truncated tetrahedra. Its vertex figure is a pentagonal pyramid, with one icosahedron on the base, and 5 truncated tetrahedra around the sides.

Alternate names

Truncated 600-cell (Norman W. Johnson)
Truncated hexacosichoron (Acronym tex) (George Olshevsky, and Jonathan Bowers)[3]
Truncated tetraplex (Conway)

Structure

The truncated 600-cell consists of 600 truncated tetrahedra and 120 icosahedra. The truncated tetrahedral cells are joined to each other via their hexagonal faces, and to the icosahedral cells via their triangular faces. Each icosahedron is surrounded by 20 truncated tetrahedra.

Images

Stereographic projection or Schlegel diagrams

Centered on icosahedron

Centered on truncated tetrahedron

Central part and some of 120 red icosahedra.

Net

Orthographic projections by Coxeter planes

H4	-	F4
[30]	[20]	[12]
H3	A2 / B3 / D4	A3 / B2
[10]	[6]	[4]

3D Parallel projection
	Parallel projection into 3 dimensions, centered on an icosahedron. Nearest icosahedron to the 4D viewpoint rendered in red, remaining icosahedra in yellow. Truncated tetrahedra in transparent green.

Related polytopes

H4 family polytopes
120-cell	rectified 120-cell	truncated 120-cell	cantellated 120-cell	runcinated 120-cell	cantitruncated 120-cell	runcitruncated 120-cell	omnitruncated 120-cell
{5,3,3}	r{5,3,3}	t{5,3,3}	rr{5,3,3}	t0,3{5,3,3}	tr{5,3,3}	t0,1,3{5,3,3}	t0,1,2,3{5,3,3}
600-cell	rectified 600-cell	truncated 600-cell	cantellated 600-cell	bitruncated 600-cell	cantitruncated 600-cell	runcitruncated 600-cell	omnitruncated 600-cell
{3,3,5}	r{3,3,5}	t{3,3,5}	rr{3,3,5}	2t{3,3,5}	tr{3,3,5}	t0,1,3{3,3,5}	t0,1,2,3{3,3,5}

Notes

Klitizing, (o3o3x5x - thi)
Klitizing, (o3x3x5o - xhi)

Klitizing, (x3x3o5o - tex)

References

Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6
(Paper 22) H.S.M. Coxeter, Regular and Semi-Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
(Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
(Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
J.H. Conway and M.J.T. Guy: Four-Dimensional Archimedean Polytopes, Proceedings of the Colloquium on Convexity at Copenhagen, page 38 und 39, 1965
N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966
Four-dimensional Archimedean Polytopes (German), Marco Möller, 2004 PhD dissertation [1] m58 m59 m53
Convex uniform polychora based on the hecatonicosachoron (120-cell) and hexacosichoron (600-cell) - Model 36, 39, 41, George Olshevsky.
Klitzing, Richard. "4D uniform polytopes (polychora)". o3o3x5x - thi, o3x3x5o - xhi, x3x3o5o - tex
Four-Dimensional Polytope Projection Barn Raisings (A Zometool construction of the truncated 120-cell), George W. Hart

External links

H4 uniform polytopes with coordinates: t{3,3,5} t{5,3,3} 2t{5,3,3}

Fundamental convex regular and uniform polytopes in dimensions 2–10
Family	An	Bn	I2(p) / Dn	E6 / E7 / E8 / F4 / G2	Hn
Regular polygon	Triangle	Square	p-gon	Hexagon	Pentagon
Uniform polyhedron	Tetrahedron	Octahedron • Cube	Demicube		Dodecahedron • Icosahedron
Uniform 4-polytope	5-cell	16-cell • Tesseract	Demitesseract	24-cell	120-cell • 600-cell
Uniform 5-polytope	5-simplex	5-orthoplex • 5-cube	5-demicube
Uniform 6-polytope	6-simplex	6-orthoplex • 6-cube	6-demicube	122 • 221
Uniform 7-polytope	7-simplex	7-orthoplex • 7-cube	7-demicube	132 • 231 • 321
Uniform 8-polytope	8-simplex	8-orthoplex • 8-cube	8-demicube	142 • 241 • 421
Uniform 9-polytope	9-simplex	9-orthoplex • 9-cube	9-demicube
Uniform 10-polytope	10-simplex	10-orthoplex • 10-cube	10-demicube
Uniform n-polytope	n-simplex	n-orthoplex • n-cube	n-demicube	1k2 • 2k1 • k21	n-pentagonal polytope
Topics: Polytope families • Regular polytope • List of regular polytopes and compounds

Undergraduate Texts in Mathematics

Graduate Texts in Mathematics

Graduate Studies in Mathematics

Mathematics Encyclopedia

World

Index

Hellenica World - Scientific Library

Retrieved from "http://en.wikipedia.org/"
All text is available under the terms of the GNU Free Documentation License