In geometry, the trioctagonal tiling is a semiregular tiling of the hyperbolic plane, representing a rectified Order-3 octagonal tiling. There are two triangles and two octagons alternating on each vertex. It has Schläfli symbol of r{8,3}.
Symmetry
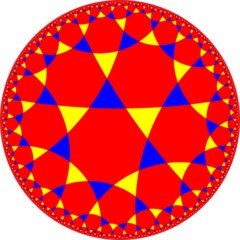 The half symmetry [1+,8,3] = [(4,3,3)] can be shown with alternating two colors of triangles, by Coxeter diagram |
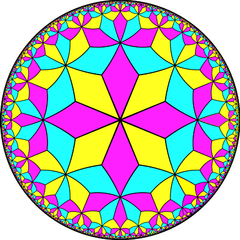 Dual tiling |
Dual tiling
Related polyhedra and tilings
From a Wythoff construction there are eight hyperbolic uniform tilings that can be based from the regular octagonal tiling.
Drawing the tiles colored as red on the original faces, yellow at the original vertices, and blue along the original edges, there are 8 forms.
| Uniform octagonal/triangular tilings
|
|||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Symmetry: [8,3], (*832) | [8,3]+ (832) |
[1+,8,3] (*443) |
[8,3+] (3*4) |
||||||||||
| {8,3} | t{8,3} | r{8,3} | t{3,8} | {3,8} | rr{8,3} s2{3,8} |
tr{8,3} | sr{8,3} | h{8,3} | h2{8,3} | s{3,8} | |||
| Uniform duals | |||||||||||||
| V83 | V3.16.16 | V3.8.3.8 | V6.6.8 | V38 | V3.4.8.4 | V4.6.16 | V34.8 | V(3.4)3 | V8.6.6 | V35.4 | |||
It can also be generated from the (4 3 3) hyperbolic tilings:
| Uniform (4,3,3) tilings
|
|||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Symmetry: [(4,3,3)], (*433) | [(4,3,3)]+, (433) | ||||||||||
 |
 |
 |
 |
 |
 |
 |
 |
||||
| h{8,3} t0(4,3,3) |
r{3,8}1/2 t0,1(4,3,3) |
h{8,3} t1(4,3,3) |
h2{8,3} t1,2(4,3,3) |
{3,8}1/2 t2(4,3,3) |
h2{8,3} t0,2(4,3,3) |
t{3,8}1/2 t0,1,2(4,3,3) |
s{3,8}1/2 s(4,3,3) |
||||
| Uniform duals | |||||||||||
 |
 |
 |
 |
 |
 |
 |
 |
||||
| V(3.4)3 | V3.8.3.8 | V(3.4)3 | V3.6.4.6 | V(3.3)4 | V3.6.4.6 | V6.6.8 | V3.3.3.3.3.4 | ||||
The trioctagonal tiling can be seen in a sequence of quasiregular polyhedrons and tilings:
| Quasiregular tilings: (3.n)2
|
||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sym. *n32 [n,3] |
Spherical | Euclid. | Compact hyperb. | Paraco. | Noncompact hyperbolic | |||||||
| *332 [3,3] Td |
*432 [4,3] Oh |
*532 [5,3] Ih |
*632 [6,3] p6m |
*732 [7,3] |
*832 [8,3]... |
*∞32 [∞,3] |
[12i,3] | [9i,3] | [6i,3] | |||
| Figure |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
||
| Figure |
 |
 |
 |
 |
||||||||
| Vertex | (3.3)2 | (3.4)2 | (3.5)2 | (3.6)2 | (3.7)2 | (3.8)2 | (3.∞)2 | (3.12i)2 | (3.9i)2 | (3.6i)2 | ||
| Schläfli | r{3,3} | r{3,4} | r{3,5} | r{3,6} | r{3,7} | r{3,8} | r{3,∞} | r{3,12i} | r{3,9i} | r{3,6i} | ||
| Coxeter |
||||||||||||
| Dual uniform figures | ||||||||||||
| Dual conf. |
 V(3.3)2 |
 V(3.4)2 |
 V(3.5)2 |
 V(3.6)2 |
 V(3.7)2 |
 V(3.8)2 |
 V(3.∞)2 |
|||||
| Dimensional family of quasiregular polyhedra and tilings: (8.n)2
|
|||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Symmetry *8n2 [n,8] |
Hyperbolic... | Paracompact | Noncompact | ||||||||
| *832 [3,8] |
*842 [4,8] |
*852 [5,8] |
*862 [6,8] |
*872 [7,8] |
*882 [8,8]... |
*∞82 [∞,8] |
[iπ/λ,8] |
||||
| Coxeter | |||||||||||
| Quasiregular figures configuration |
 3.8.3.8 |
 4.8.4.8 |
 8.5.8.5 |
 8.6.8.6 |
 8.7.8.7 |
 8.8.8.8 |
 8.∞.8.∞ |
8.∞.8.∞ |
|||
See also
Trihexagonal tiling - 3.6.3.6 tiling
Rhombille tiling - dual V3.6.3.6 tiling
Tilings of regular polygons
List of uniform tilings
References
John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 19, The Hyperbolic Archimedean Tessellations)
"Chapter 10: Regular honeycombs in hyperbolic space". The Beauty of Geometry: Twelve Essays. Dover Publications. 1999. ISBN 0-486-40919-8. LCCN 99035678.
Undergraduate Texts in Mathematics
Graduate Studies in Mathematics
Hellenica World - Scientific Library
Retrieved from "http://en.wikipedia.org/"
All text is available under the terms of the GNU Free Documentation License

