The tetrated dodecahedron is a near-miss Johnson solid. It was first discovered in 2002 by Alex Doskey. It was then independently rediscovered in 2003 and named by Robert Austin.[1]
It has 28 faces: twelve regular pentagons arranged in four panels of three pentagons each, four equilateral triangles (shown in blue), and six pairs of isosceles triangles (shown in yellow). All edges of the tetrated dodecahedron have the same length, except for the shared bases of these isosceles triangles, which are approximately 1.07 times as long as the other edges. This polyhedron has tetrahedral symmetry.
Topologically, as a near-miss Johnson solid, the four triangles corresponding to the face planes of a tetrahedron are always equilateral, while the pentagons and the other triangles only have reflection symmetry.
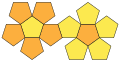
Net
The 12 pentagons and 16 triangles are colored in this net by their locations within the tetrahedral symmetry.
| Dodecahedron (Platonic solid) |
Icosidodecahedron (Archimedean solid) |
Pentagonal orthobirotunda (Johnson solid) |
|---|---|---|
 |
 |
 |
 |
 |
 |
See also
Tetrahedrally diminished dodecahedron
Notes
Tetrated dodecahedra
vte
Near-miss Johnson solids
Truncated forms
Truncated triakis tetrahedron Chamfered cube (Truncated rhombic dodecahedron) Chamfered dodecahedron (Truncated rhombic triacontahedron)
Other forms
Tetrated dodecahedron Rectified truncated icosahedron Pentahexagonal pyritoheptacontatetrahedron
Undergraduate Texts in Mathematics
Graduate Studies in Mathematics
Hellenica World - Scientific Library
Retrieved from "http://en.wikipedia.org/"
All text is available under the terms of the GNU Free Documentation License


