In geometry, a tetrakis hexahedron (also known as a tetrahexahedron, hextetrahedron, tetrakis cube, and kiscube[2]) is a Catalan solid. Its dual is the truncated octahedron, an Archimedean solid.
It also can be called a disdyakis hexahedron or hexakis tetrahedron as the dual of an omnitruncated tetrahedron.
Cartesian coordinates
Cartesian coordinates for the 14 vertices of a tetrakis hexahedron centered at the origin, are the points (±3/2, 0, 0), (0, ±3/2, 0), (0, 0, ±3/2) and (±1, ±1, ±1).
The length of the shorter edges of this tetrakis hexahedron equals 3/2 and that of the longer edges equals 2. The faces are acute isosceles triangles. The larger angle of these equals {\displaystyle \arccos(1/9)\approx 83.620\,629\,791\,56^{\circ }} and the two smaller ones equal arccos {\displaystyle \arccos(2/3)\approx 48.189\,685\,104\,22^{\circ }}.
Orthogonal projections
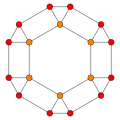
The tetrakis hexahedron, dual of the truncated octahedron has 3 symmetry positions, two located on vertices and one mid-edge.
| Projective symmetry |
[2] | [4] | [6] |
|---|---|---|---|
| Tetrakis hexahedron |
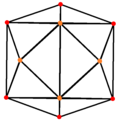 |
 |
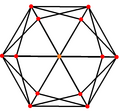 |
| Truncated octahedron |
 |
 |
 |
Uses
Naturally occurring (crystal) formations of tetrahexahedra are observed in copper and fluorite systems.
Polyhedral dice shaped like the tetrakis hexahedron are occasionally used by gamers.
A 24-cell viewed under a vertex-first perspective projection has a surface topology of a tetrakis hexahedron and the geometric proportions of the rhombic dodecahedron, with the rhombic faces divided into two triangles.
The tetrakis hexahedron appears as one of the simplest examples in building theory. Consider the Riemannian symmetric space associated to the group SL4(R). Its Tits boundary has the structure of a spherical building whose apartments are 2-dimensional spheres. The partition of this sphere into spherical simplices (chambers) can be obtained by taking the radial projection of a tetrakis hexahedron.
Symmetry
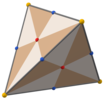
With Td, [3,3] (*332) tetrahedral symmetry, the triangular faces represent the 24 fundamental domains of tetrahedral symmetry. This polyhedron can be constructed from 6 great circles on a sphere. It can also be seen by a cube with its square faces triangulated by their vertices and face centers and a tetrahedron with its faces divided by vertices, mid-edges, and a central point.
 |
 |
 |
 |
 |
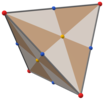 |
| Truncated tetratetrahedron |
Disdyakis hexahedron |
Deltoidal dodecahedron |
Rhombic hexahedron |
Tetrahedron | |
| Spherical polyhedron | |||
|---|---|---|---|
 |
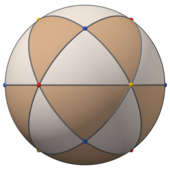 |
 |
 |
| (see rotating model) | Orthographic projections from 2-, 3- and 4-fold axes | ||
The edges of the spherical tetrakis hexahedron belong to six great circles, which correspond to mirror planes in tetrahedral symmetry. They can be grouped into three pairs of orthogonal circles (which typically intersect on one coordinate axis each). In the images below these square hosohedra are colored red, green and blue.
| Stereographic projections | |||
|---|---|---|---|
 |
2-fold | 3-fold | 4-fold |
 |
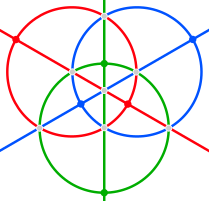 |
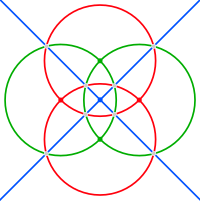 |
|
Dimensions
If we denote the edge length of the base cube by a, the height of each pyramid summit above the cube is a/4. The inclination of each triangular face of the pyramid versus the cube face is arctan(1/2), approximately 26.565° (sequence A073000 in the OEIS). One edge of the isosceles triangles has length a, the other two have length 3a/4, which follows by applying the Pythagorean theorem to height and base length. This yields an altitude of √5a/4 in the triangle (OEIS: A204188). Its area is √5a/8, and the internal angles are arccos(2/3) (approximately 48.1897°) and the complementary 180° − 2 arccos(2/3) (approximately 83.6206°).
The volume of the pyramid is a3/12; so the total volume of the six pyramids and the cube in the hexahedron is 3a3/2.
Kleetope
It can be seen as a cube with square pyramids covering each square face; that is, it is the Kleetope of the cube.
Cubic pyramid
It is very similar to the 3D net for a 4D cubic pyramid, as the net for a square based is a square with triangles attached to each edge, the net for a cubic pyramid is a cube with square pyramids attached to each face.
Related polyhedra and tilings
| Uniform octahedral polyhedra | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Symmetry: [4,3], (*432) | [4,3]+ (432) |
[1+,4,3] = [3,3] (*332) |
[3+,4] (3*2) |
|||||||
| {4,3} | t{4,3} | r{4,3} r{31,1} |
t{3,4} t{31,1} |
{3,4} {31,1} |
rr{4,3} s2{3,4} |
tr{4,3} | sr{4,3} | h{4,3} {3,3} |
h2{4,3} t{3,3} |
s{3,4} s{31,1} |
= |
= |
= |
||||||||
| Duals to uniform polyhedra | ||||||||||
| V43 | V3.82 | V(3.4)2 | V4.62 | V34 | V3.43 | V4.6.8 | V34.4 | V33 | V3.62 | V35 |
| *n32 symmetry mutation of truncated tilings: n.6.6
|
||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sym. *n42 [n,3] |
Spherical | Euclid. | Compact | Parac. | Noncompact hyperbolic | |||||||
| *232 [2,3] |
*332 [3,3] |
*432 [4,3] |
*532 [5,3] |
*632 [6,3] |
*732 [7,3] |
*832 [8,3]... |
*∞32 [∞,3] |
[12i,3] | [9i,3] | [6i,3] | ||
| Truncated figures |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
|
| Config. | 2.6.6 | 3.6.6 | 4.6.6 | 5.6.6 | 6.6.6 | 7.6.6 | 8.6.6 | ∞.6.6 | 12i.6.6 | 9i.6.6 | 6i.6.6 | |
| n-kis figures |
 |
 |
 |
 |
 |
 |
 |
|||||
| Config. | V2.6.6 | V3.6.6 | V4.6.6 | V5.6.6 | V6.6.6 | V7.6.6 | V8.6.6 | V∞.6.6 | V12i.6.6 | V9i.6.6 | V6i.6.6 | |
It is a polyhedra in a sequence defined by the face configuration V4.6.2n. This group is special for having all even number of edges per vertex and form bisecting planes through the polyhedra and infinite lines in the plane, and continuing into the hyperbolic plane for any n ≥ 7.
With an even number of faces at every vertex, these polyhedra and tilings can be shown by alternating two colors so all adjacent faces have different colors.
Each face on these domains also corresponds to the fundamental domain of a symmetry group with order 2,3,n mirrors at each triangle face vertex.
| *n32 symmetry mutations of omnitruncated tilings: 4.6.2n
|
||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sym. *n32 [n,3] |
Spherical | Euclid. | Compact hyperb. | Paraco. | Noncompact hyperbolic | |||||||
| *232 [2,3] |
*332 [3,3] |
*432 [4,3] |
*532 [5,3] |
*632 [6,3] |
*732 [7,3] |
*832 [8,3] |
*∞32 [∞,3] |
[12i,3] |
[9i,3] |
[6i,3] |
[3i,3] |
|
| Figures |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
|
| Config. | 4.6.4 | 4.6.6 | 4.6.8 | 4.6.10 | 4.6.12 | 4.6.14 | 4.6.16 | 4.6.∞ | 4.6.24i | 4.6.18i | 4.6.12i | 4.6.6i |
| Duals |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
| Config. | V4.6.4 | V4.6.6 | V4.6.8 | V4.6.10 | V4.6.12 | V4.6.14 | V4.6.16 | V4.6.∞ | V4.6.24i | V4.6.18i | V4.6.12i | V4.6.6i |
See also
Disdyakis triacontahedron
Disdyakis dodecahedron
Kisrhombille tiling
Compound of three octahedra
Deltoidal icositetrahedron, another 24-face Catalan solid.
References
Hexakistetraeder in German, see e.g. Meyers page and Brockhaus page. The same drawing appears in Brockhaus and Efron as преломленный пирамидальный тетраэдр (refracted pyramidal tetrahedron).
Conway, Symmetries of Things, p.284
Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X. (Section 3-9)
Wenninger, Magnus (1983), Dual Models, Cambridge University Press, doi:10.1017/CBO9780511569371, ISBN 978-0-521-54325-5, MR 0730208 (The thirteen semiregular convex polyhedra and their duals, Page 14, Tetrakishexahedron)
The Symmetries of Things 2008, John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, ISBN 978-1-56881-220-5 [1] (Chapter 21, Naming the Archimedean and Catalan polyhedra and tilings, page 284, Tetrakis hexahedron)
External links
Eric W. Weisstein, Tetrakis hexahedron (Catalan solid) at MathWorld.
Virtual Reality Polyhedra www.georgehart.com: The Encyclopedia of Polyhedra
VRML model
Conway Notation for Polyhedra Try: "dtO" or "kC"
Tetrakis Hexahedron – Interactive Polyhedron model
The Uniform Polyhedra
vte
|
Catalan solids
|
|||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|||||||||||||||||||||||||||
|
Archimedean duals
|
|||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|||||||||||||||||||||||||||
Convex polyhedra
Platonic solids (regular)
tetrahedron cube octahedron dodecahedron icosahedron
Archimedean solids
(semiregular or uniform)
truncated tetrahedron cuboctahedron truncated cube truncated octahedron rhombicuboctahedron truncated cuboctahedron snub cube icosidodecahedron truncated dodecahedron truncated icosahedron rhombicosidodecahedron truncated icosidodecahedron snub dodecahedron
Catalan solids
(duals of Archimedean)
triakis tetrahedron rhombic dodecahedron triakis octahedron tetrakis hexahedron deltoidal icositetrahedron disdyakis dodecahedron pentagonal icositetrahedron rhombic triacontahedron triakis icosahedron pentakis dodecahedron deltoidal hexecontahedron disdyakis triacontahedron pentagonal hexecontahedron
Dihedral regular
dihedron hosohedron
Dihedral uniform
prisms antiprisms
duals:
bipyramids trapezohedra
Dihedral others
pyramids truncated trapezohedra gyroelongated bipyramid cupola bicupola pyramidal frusta bifrustum rotunda birotunda prismatoid scutoid
Degenerate polyhedra are in italics.
Undergraduate Texts in Mathematics
Graduate Studies in Mathematics
Hellenica World - Scientific Library
Retrieved from "http://en.wikipedia.org/"
All text is available under the terms of the GNU Free Documentation License











































