In 4-dimensional geometry, the tetrahedral cupola is a polychoron bounded by one tetrahedron, a parallel cuboctahedron, connected by 10 triangular prisms, and 4 triangular pyramids.[1]
Related polytopes
The tetrahedral cupola can be sliced off from a runcinated 5-cell, on a hyperplane parallel to a tetrahedral cell. The cuboctahedron base passes through the center of the runcinated 5-cell, so the Tetrahedral cupola contains half of the tetrahedron and triangular prism cells of the runcinated 5-cell. The cupola can be seen in A2 and A3 Coxeter plane orthogonal projection of the runcinated 5-cell:
| A3 Coxeter plane | ||
|---|---|---|
| Runcinated 5-cell | Tetrahedron (Cupola top) |
Cuboctahedron (Cupola base) |
 |
 |
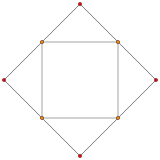 |
| A2 Coxeter plane | ||
 |
 |
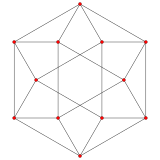 |
See also
Tetrahedral pyramid (5-cell)
References
Convex Segmentochora Dr. Richard Klitzing, Symmetry: Culture and Science, Vol. 11, Nos. 1-4, 139-181, 2000 (4.23 tetrahedron || cuboctahedron)
External links
Segmentochora: tetaco, tet || co, K-4.23
Undergraduate Texts in Mathematics
Graduate Studies in Mathematics
Hellenica World - Scientific Library
Retrieved from "http://en.wikipedia.org/"
All text is available under the terms of the GNU Free Documentation License

