Surface triangulation

Triangulation of a surface means

a net of triangles, which covers a given surface partly or totally, or
the procedure of generating the points and triangles of such a net of triangles.

Triangulation of an implicit surface of genus 3

Approaches

This article describes the generation of a net of triangles. In literature there are contributions which deal with the optimization of a given net.

Surface triangulations are important for

visualizing surfaces and
the application of finite element methods.

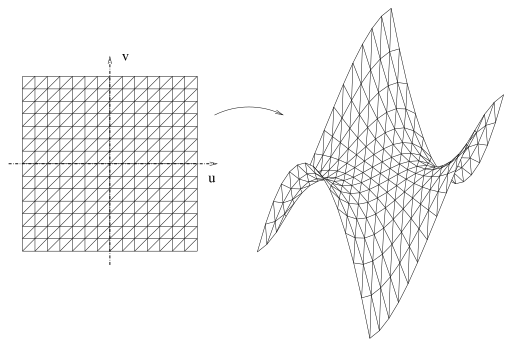
The triangulation of a parametrically defined surface is simply achieved by triangulating the area of definition (see second figure, depicting the Monkey Saddle). However, the triangles may vary in shape and extension in object space, posing a potential drawback. This can be minimized through adaptive methods that consider step width while triangulating the parameter area.

Triangulation of a parametric surface (Monkey Saddle)

To triangulate an implicit surface (defined by one or more equations) is more difficult. There exist essentially two methods.

One method divides the 3D region of consideration into cubes and determines the intersections of the surface with the edges of the cubes in order to get polygons on the surface, which thereafter have to be triangulated (cutting cube method).[1][2] The expenditure for managing the data is great.
The second and simpler concept is the marching method.[3][4][5] The triangulation starts with a triangulated hexagon at a starting point. This hexagon is then surrounded by new triangles, following given rules, until the surface of consideration is triangulated. If the surface consists of several components, the algorithm has to be started several times using suitable starting points.

The cutting cube algorithm determines, at the same time, all components of the surface within the surrounding starting cube depending on prescribed limit parameters. An advantage of the marching method is the possibility to prescribe boundaries (see picture).

Polygonizing a surface means to generate a polygon mesh.

The triangulation of a surface should not be confused with the triangulation of a discrete prescribed plane set of points. See Delaunay triangulation.

Triangulation: cylinder, surface \( x^{4}+y^{4}+z^{4}=1 \)

Torus: triangulated by the marching method

Torus: polygonized by the cutting cube method