In complex analysis, a discipline within mathematics, the residue theorem, sometimes called Cauchy's residue theorem, is a powerful tool to evaluate line integrals of analytic functions over closed curves; it can often be used to compute real integrals and infinite series as well. It generalizes the Cauchy integral theorem and Cauchy's integral formula. From a geometrical perspective, it is a special case of the generalized Stokes' theorem.
Statement
The statement is as follows:
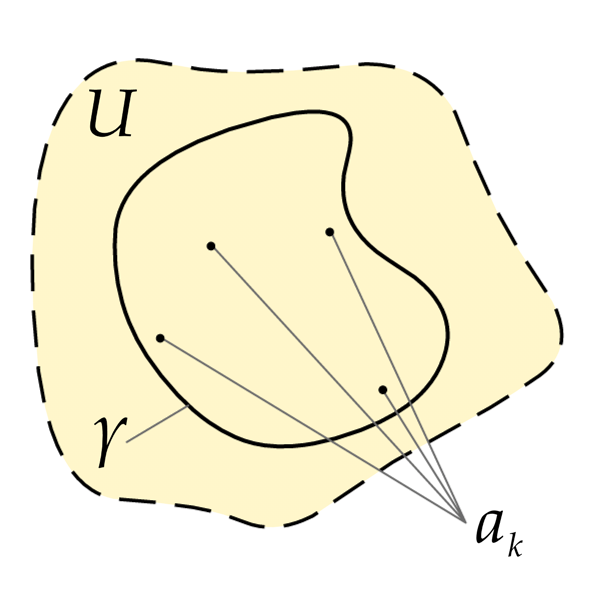
Illustration of the setting.
Let U be a simply connected open subset of the complex plane containing a finite list of points a1, ..., an, and f a function defined and holomorphic on U \{a1, ..., an}. Let γ be a closed rectifiable curve in U which does not meet any of the ak, and denote the winding number of γ around ak by I(γ, ak). The line integral of f around γ is equal to 2πi times the sum of residues of f at the points, each counted as many times as γ winds around the point:
\( {\displaystyle \oint _{\gamma }f(z)\,dz=2\pi i\sum _{k=1}^{n}\operatorname {I} (\gamma ,a_{k})\operatorname {Res} (f,a_{k}).} \)
If γ is a positively oriented simple closed curve, I(γ, ak) = 1 if ak is in the interior of γ, and 0 if not, so
\( {\displaystyle \oint _{\gamma }f(z)\,dz=2\pi i\sum \operatorname {Res} (f,a_{k})} \)
with the sum over those ak inside γ.
The relationship of the residue theorem to Stokes' theorem is given by the Jordan curve theorem. The general plane curve γ must first be reduced to a set of simple closed curves {γi} whose total is equivalent to γ for integration purposes; this reduces the problem to finding the integral of f dz along a Jordan curve γi with interior V. The requirement that f be holomorphic on U0 = U \ {ak} is equivalent to the statement that the exterior derivative d(f dz) = 0 on U0. Thus if two planar regions V and W of U enclose the same subset {aj} of {ak}, the regions V \ W and W \ V lie entirely in U0, and hence
\( {\displaystyle \int _{V\smallsetminus W}d(f\,dz)-\int _{W\smallsetminus V}d(f\,dz)} \)
is well-defined and equal to zero. Consequently, the contour integral of f dz along γj = ∂V is equal to the sum of a set of integrals along paths λj, each enclosing an arbitrarily small region around a single aj — the residues of f (up to the conventional factor 2πi) at {aj}. Summing over {γj}, we recover the final expression of the contour integral in terms of the winding numbers {I(γ, ak)}.
In order to evaluate real integrals, the residue theorem is used in the following manner: the integrand is extended to the complex plane and its residues are computed (which is usually easy), and a part of the real axis is extended to a closed curve by attaching a half-circle in the upper or lower half-plane, forming a semicircle. The integral over this curve can then be computed using the residue theorem. Often, the half-circle part of the integral will tend towards zero as the radius of the half-circle grows, leaving only the real-axis part of the integral, the one we were originally interested in.
Examples
An integral along the real axis
The integral
\( {\displaystyle \int _{-\infty }^{\infty }{\frac {e^{itx}}{x^{2}+1}}\,dx} \)
The contour C.
arises in probability theory when calculating the characteristic function of the Cauchy distribution. It resists the techniques of elementary calculus but can be evaluated by expressing it as a limit of contour integrals.
Suppose t > 0 and define the contour C that goes along the real line from −a to a and then counterclockwise along a semicircle centered at 0 from a to −a. Take a to be greater than 1, so that the imaginary unit i is enclosed within the curve. Now consider the contour integral
\( {\displaystyle \int _{C}{f(z)}\,dz=\int _{C}{\frac {e^{itz}}{z^{2}+1}}\,dz.} \)
Since eitz is an entire function (having no singularities at any point in the complex plane), this function has singularities only where the denominator z2 + 1 is zero. Since z2 + 1 = (z + i)(z − i), that happens only where z = i or z = −i. Only one of those points is in the region bounded by this contour. Because f(z) is
\( {\begin{aligned}{\frac {e^{itz}}{z^{2}+1}}&={\frac {e^{itz}}{2i}}\left({\frac {1}{z-i}}-{\frac {1}{z+i}}\right)\\&={\frac {e^{itz}}{2i(z-i)}}-{\frac {e^{itz}}{2i(z+i)}},\end{aligned}} \)
the residue of f(z) at z = i is
\( {\displaystyle \operatorname {Res} \limits _{z=i}f(z)={\frac {e^{-t}}{2i}}.} \)
According to the residue theorem, then, we have
\( {\displaystyle \int _{C}f(z)\,dz=2\pi i\cdot \operatorname {Res} \limits _{z=i}f(z)=2\pi i{\frac {e^{-t}}{2i}}=\pi e^{-t}.} \)
The contour C may be split into a straight part and a curved arc, so that
\( \int _{\mathrm {straight} }f(z)\,dz+\int _{\mathrm {arc} }f(z)\,dz=\pi e^{-t}\, \)
and thus
\( \int _{-a}^{a}f(z)\,dz=\pi e^{-t}-\int _{\mathrm {arc} }f(z)\,dz. \)
Using some estimations, we have
\( {\displaystyle \left|\int _{\mathrm {arc} }{\frac {e^{itz}}{z^{2}+1}}\,dz\right|\leq \pi a\cdot \sup _{\text{arc}}\left|{\frac {e^{itz}}{z^{2}+1}}\right|\leq \pi a\cdot \sup _{\text{arc}}{\frac {1}{|z^{2}+1|}}\leq {\frac {\pi a}{a^{2}-1}},} \)
and
\( {\displaystyle \lim _{a\to \infty }{\frac {\pi a}{a^{2}-1}}=0.} \)
The estimate on the numerator follows since t > 0, and for complex numbers z along the arc (which lies in the upper halfplane), the argument φ of z lies between 0 and π. So,
\( \left|e^{itz}\right|=\left|e^{it|z|(\cos \phi +i\sin \phi )}\right|=\left|e^{-t|z|\sin \phi +it|z|\cos \phi }\right|=e^{-t|z|\sin \phi }\leq 1.
Therefore,
\( {\displaystyle \int _{-\infty }^{\infty }{\frac {e^{itz}}{z^{2}+1}}\,dz=\pi e^{-t}.} \)
If t < 0 then a similar argument with an arc C′ that winds around −i rather than i shows that
The contour C′.
\( {\displaystyle \int _{-\infty }^{\infty }{\frac {e^{itz}}{z^{2}+1}}\,dz=\pi e^{t},} \)
and finally we have
\( {\displaystyle \int _{-\infty }^{\infty }{\frac {e^{itz}}{z^{2}+1}}\,dz=\pi e^{-\left|t\right|}.} \)
(If t = 0 then the integral yields immediately to elementary calculus methods and its value is π.)
An infinite sum
The fact that π cot(πz) has simple poles with residue 1 at each integer can be used to compute the sum
\( {\displaystyle \displaystyle \sum _{n=-\infty }^{\infty }f(n).} \)
Consider, for example, f(z) = z−2. Let ΓN be the rectangle that is the boundary of [−N − 1/2, N + 1/2]2 with positive orientation, with an integer N. By the residue formula,
\( {\displaystyle {\frac {1}{2\pi i}}\int _{\Gamma _{N}}f(z)\pi \cot(\pi z)\,dz=\operatorname {Res} \limits _{z=0}+\sum _{n=-N \atop n\neq 0}^{N}n^{-2}.} \)
The left-hand side goes to zero as N → ∞ since the integrand has order O(N−2). On the other hand,[1]
\( {\displaystyle {\frac {z}{2}}\cot \left({\frac {z}{2}}\right)=1-B_{2}{\frac {z^{2}}{2!}}+\cdots ;\qquad B_{2}={\frac {1}{6}}.} \)
(In fact, z/2 cot(z/2) = iz/1 − e−iz − iz/2.) Thus, the residue Resz=0 is −π2/3. We conclude:
\( {\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n^{2}}}={\frac {\pi ^{2}}{6}}} \)
which is a proof of the Basel problem.
The same trick can be used to establish the sum of the Eisenstein series:
\( {\displaystyle \pi \cot(\pi z)=\lim _{N\to \infty }\sum _{n=-N}^{N}(z-n)^{-1}.} \)
We take f(z) = (w − z)−1 with w a non-integer and we shall show the above for w. The difficulty in this case is to show the vanishing of the contour integral at infinity. We have:
\( {\displaystyle \int _{\Gamma _{N}}{\frac {\pi \cot(\pi z)}{z}}\,dz=0} \)
since the integrand is an even function and so the contributions from the contour in the left-half plane and the contour in the right cancel each other out. Thus,
\( {\displaystyle \int _{\Gamma _{N}}f(z)\pi \cot(\pi z)\,dz=\int _{\Gamma _{N}}\left({\frac {1}{w-z}}+{\frac {1}{z}}\right)\pi \cot(\pi z)\,dz} \)
goes to zero as N → ∞.
See also
Cauchy's integral formula
Glasser's master theorem
Jordan's lemma
Methods of contour integration
Morera's theorem
Nachbin's theorem
Residue at infinity
Logarithmic form
References
Whittaker, E. T.; Watson, G. N. (1902). A Course of Modern Analysis. Cambridge University Press. § 7.2.
Ahlfors, Lars (1979), Complex Analysis, McGraw Hill, ISBN 0-07-085008-9
Mitrinović, Dragoslav; Kečkić, Jovan (1984), The Cauchy method of residues: Theory and applications, D. Reidel Publishing Company, ISBN 90-277-1623-4
Lindelöf, Ernst (1905), Le calcul des résidus et ses applications à la théorie des fonctions, Editions Jacques Gabay (published 1989), ISBN 2-87647-060-8
External links
"Cauchy integral theorem", Encyclopedia of Mathematics, EMS Presss, 2001 [1994]
Residue theorem in MathWorld
Undergraduate Texts in Mathematics
Graduate Studies in Mathematics
Hellenica World - Scientific Library
Retrieved from "http://en.wikipedia.org/"
All text is available under the terms of the GNU Free Documentation License