In the geometry of hyperbolic 3-space, the order-3-6 heptagonal honeycomb a regular space-filling tessellation (or honeycomb). Each infinite cell consists of a heptagonal tiling whose vertices lie on a 2-hypercycle, each of which has a limiting circle on the ideal sphere.
| Order-3-6 heptagonal honeycomb | |
|---|---|
| Type | Regular honeycomb |
| Schläfli symbol | {7,3,6} {7,3[3]} |
| Coxeter diagram | |
| Cells | {7,3}  |
| Faces | {7} |
| Vertex figure | {3,6} |
| Dual | {6,3,7} |
| Coxeter group | [7,3,6] [7,3[3]] |
| Properties | Regular |
Geometry
The Schläfli symbol of the order-3-6 heptagonal honeycomb is {7,3,6}, with six heptagonal tilings meeting at each edge. The vertex figure of this honeycomb is an triangular tiling, {3,6}.
It has a quasiregular construction, ![]()
![]()
![]()
![]()
![]() , which can be seen as alternately colored cells.
, which can be seen as alternately colored cells.
 Poincaré disk model |
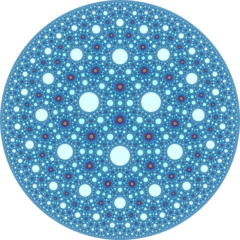 Ideal surface |
Related polytopes and honeycombs
It is a part of a series of regular polytopes and honeycombs with {p,3,6} Schläfli symbol, and triangular tiling vertex figures.
| Form | Paracompact | Noncompact | |||||
|---|---|---|---|---|---|---|---|
| Name | {3,3,6} {3,3[3]} |
{4,3,6} {4,3[3]} |
{5,3,6} {5,3[3]} |
{6,3,6} {6,3[3]} |
{7,3,6} {7,3[3]} |
{8,3,6} {8,3[3]} |
... {∞,3,6} {∞,3[3]} |
| Image |  |
 |
 |
 |
 |
 |
 |
| Cells | {3,3} |
{4,3} |
{5,3} |
{6,3} |
{7,3} |
{8,3} |
{∞,3} |
Order-3-6 octagonal honeycomb
| Order-3-6 octagonal honeycomb | |
|---|---|
| Type | Regular honeycomb |
| Schläfli symbol | {8,3,6} {8,3[3]} |
| Coxeter diagram | |
| Cells | {8,3}  |
| Faces | Octagon {8} |
| Vertex figure | triangular tiling {3,6} |
| Dual | {6,3,8} |
| Coxeter group | [8,3,6] [8,3[3]] |
| Properties | Regular |
In the geometry of hyperbolic 3-space, the order-3-6 octagonal honeycomb a regular space-filling tessellation (or honeycomb). Each infinite cell consists of an order-6 octagonal tiling whose vertices lie on a 2-hypercycle, each of which has a limiting circle on the ideal sphere.
The Schläfli symbol of the order-3-6 octagonal honeycomb is {8,3,6}, with six octagonal tilings meeting at each edge. The vertex figure of this honeycomb is a triangular tiling, {3,6}.
It has a quasiregular construction, CDel node 1.pngCDel 8.pngCDel node.pngCDel split1.pngCDel branch.png, which can be seen as alternately colored cells.
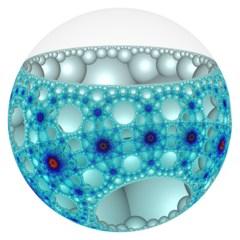
Poincaré disk model
Order-3-6 apeirogonal honeycomb
| Order-3-6 apeirogonal honeycomb | |
|---|---|
| Type | Regular honeycomb |
| Schläfli symbol | {∞,3,6} {∞,3[3]} |
| Coxeter diagram | |
| Cells | {∞,3}  |
| Faces | Apeirogon {∞} |
| Vertex figure | triangular tiling {3,6} |
| Dual | {6,3,∞} |
| Coxeter group | [∞,3,6] [∞,3[3]] |
| Properties | Regular |
In the geometry of hyperbolic 3-space, the order-3-6 apeirogonal honeycomb a regular space-filling tessellation (or honeycomb). Each infinite cell consists of an order-3 apeirogonal tiling whose vertices lie on a 2-hypercycle, each of which has a limiting circle on the ideal sphere.
The Schläfli symbol of the order-3-6 apeirogonal honeycomb is {∞,3,6}, with six order-3 apeirogonal tilings meeting at each edge. The vertex figure of this honeycomb is a triangular tiling, {3,6}.
 Poincaré disk model |
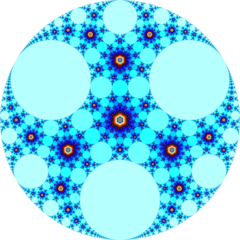 Ideal surface |
It has a quasiregular construction, CDel node 1.pngCDel infin.pngCDel node.pngCDel split1.pngCDel branch.png, which can be seen as alternately colored cells.
See also
Convex uniform honeycombs in hyperbolic space
List of regular polytopes
References
Coxeter, Regular Polytopes, 3rd. ed., Dover Publications, 1973. ISBN 0-486-61480-8. (Tables I and II: Regular polytopes and honeycombs, pp. 294–296)
The Beauty of Geometry: Twelve Essays (1999), Dover Publications, LCCN 99-35678, ISBN 0-486-40919-8 (Chapter 10, Regular Honeycombs in Hyperbolic Space) Table III
Jeffrey R. Weeks The Shape of Space, 2nd edition ISBN 0-8247-0709-5 (Chapters 16–17: Geometries on Three-manifolds I,II)
George Maxwell, Sphere Packings and Hyperbolic Reflection Groups, JOURNAL OF ALGEBRA 79,78-97 (1982) [1]
Hao Chen, Jean-Philippe Labbé, Lorentzian Coxeter groups and Boyd-Maxwell ball packings, (2013)[2]
Visualizing Hyperbolic Honeycombs arXiv:1511.02851 Roice Nelson, Henry Segerman (2015)
External links
John Baez, Visual insights: {7,3,3} Honeycomb (2014/08/01) {7,3,3} Honeycomb Meets Plane at Infinity (2014/08/14)
Danny Calegari, Kleinian, a tool for visualizing Kleinian groups, Geometry and the Imagination 4 March 2014. [3]
Undergraduate Texts in Mathematics
Graduate Studies in Mathematics
Hellenica World - Scientific Library
Retrieved from "http://en.wikipedia.org/"
All text is available under the terms of the GNU Free Documentation License

