In graph theory, a loop (also called a self-loop or a buckle) is an edge that connects a vertex to itself. A simple graph contains no loops.'
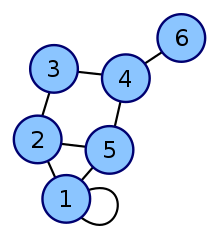
Depending on the context, a graph or a multigraph may be defined so as to either allow or disallow the presence of loops (often in concert with allowing or disallowing multiple edges between the same vertices):
Where graphs are defined so as to allow loops and multiple edges, a graph without loops or multiple edges is often distinguished from other graphs by calling it a simple graph.
Where graphs are defined so as to disallow loops and multiple edges, a graph that does have loops or multiple edges is often distinguished from the graphs that satisfy these constraints by calling it a multigraph or pseudograph.
In a graph with one vertex, all edges must be loops. Such a graph is called a bouquet.
Degree
For an undirected graph, the degree of a vertex is equal to the number of adjacent vertices.
A special case is a loop, which adds two to the degree. This can be understood by letting each connection of the loop edge count as its own adjacent vertex. In other words, a vertex with a loop "sees" itself as an adjacent vertex from both ends of the edge thus adding two, not one, to the degree.
For a directed graph, a loop adds one to the in degree and one to the out degree.
See also
In graph theory
Cycle (graph theory)
Graph theory
Glossary of graph theory
In topology
Möbius ladder
Möbius strip
Strange loop
Klein bottle
References
Balakrishnan, V. K.; Graph Theory, McGraw-Hill; 1 edition (February 1, 1997). ISBN 0-07-005489-4.
Bollobás, Béla; Modern Graph Theory, Springer; 1st edition (August 12, 2002). ISBN 0-387-98488-7.
Diestel, Reinhard; Graph Theory, Springer; 2nd edition (February 18, 2000). ISBN 0-387-98976-5.
Gross, Jonathon L, and Yellen, Jay; Graph Theory and Its Applications, CRC Press (December 30, 1998). ISBN 0-8493-3982-0.
Gross, Jonathon L, and Yellen, Jay; (eds); Handbook of Graph Theory. CRC (December 29, 2003). ISBN 1-58488-090-2.
Zwillinger, Daniel; CRC Standard Mathematical Tables and Formulae, Chapman & Hall/CRC; 31st edition (November 27, 2002). ISBN 1-58488-291-3.
External links
This article incorporates public domain material from the NIST document: Black, Paul E. "Self loop". Dictionary of Algorithms and Data Structures.
Undergraduate Texts in Mathematics
Graduate Studies in Mathematics
Hellenica World - Scientific Library
Retrieved from "http://en.wikipedia.org/"
All text is available under the terms of the GNU Free Documentation License

