In mathematics, the Griewank function is often used in testing of optimization, it is defined as follow[1]
1+{\frac {1}{4000}}\sum _{{i=1}}^{n}x_{i}^{2}-\prod _{{i=1}}^{n}\cos \left({\frac {x_{i}}{{\sqrt {i}}}}\right)
The following paragraphs display the special cases of first, second and third order Griewank function, and their plots.
First-order Griewank function
{\displaystyle g:=1+(1/4000)\cdot x_{1}^{2}-\cos(x_{1})}
First order Griewank function has multiple maxima and minima.[2]
Let the derivative of Griewank function be zero:
{\displaystyle {\frac {1}{2000}}\cdot x_{1}+\sin(x_{1})=0}
Find its roots in the interval [−100..100] by means of numerical method,
In the interval [−10000,10000], the Griewank function has 6365 critical points.
Second-order Griewank function
2nd order Griewank function 3D plot
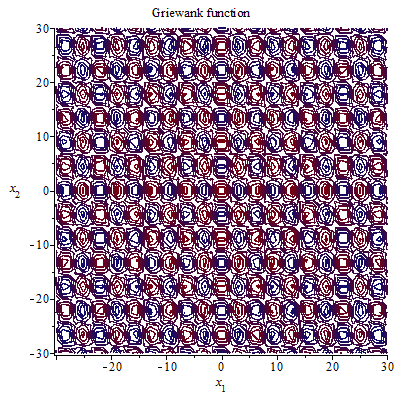
2nd-order Griewank function contour plot
1+{\frac {1}{4000}}x_{1}^{2}+{\frac {1}{4000}}x_{2}^{2}-\cos(x_{1})\cos \left({\frac 12}x_{2}{\sqrt {2}}\right)
Third order Griewank function
Third-order Griewank function Maple animation
\left\{1+{\frac {1}{4000}}\,x_{1}^{2}+{\frac {1}{4000}}\,x_{2}^{2}+{\frac {1}{4000}}\,{x_{{{3}}}}^{{2}}-\cos(x_{1})\cos \left({\frac 12}x_{2}{\sqrt {2}}\right)\cos \left({\frac 13}x_{3}{\sqrt {3}}\right)\right\}
References
Griewank, A. O. "Generalized Decent for Global Optimization." J. Opt. Th. Appl. 34, 11–39, 1981
Locatelli, M. "A Note on the Griewank Test Function." J. Global Opt. 25, 169–174, 2003
Undergraduate Texts in Mathematics
Graduate Studies in Mathematics
Hellenica World - Scientific Library
Retrieved from "http://en.wikipedia.org/"
All text is available under the terms of the GNU Free Documentation License