Gaussian curvature

In differential geometry, the Gaussian curvature or Gauss curvature Κ of a surface at a point is the product of the principal curvatures, κ1 and κ2, at the given point:

\( {\displaystyle K=\kappa _{1}\kappa _{2}.} \)

For example, a sphere of radius r has Gaussian curvature 1/r2 everywhere, and a flat plane and a cylinder have Gaussian curvature zero everywhere. The Gaussian curvature can also be negative, as in the case of a hyperboloid or the inside of a torus.

From left to right: a surface of negative Gaussian curvature (hyperboloid), a surface of zero Gaussian curvature (cylinder), and a surface of positive Gaussian curvature (sphere).

Gaussian curvature is an intrinsic measure of curvature, depending only on distances that are measured on the surface, not on the way it is isometrically embedded in Euclidean space. This is the content of the Theorema egregium.

Some points on the torus have positive, some have negative, and some have zero Gaussian curvature.

Gaussian curvature is named after Carl Friedrich Gauss, who published the Theorema egregium in 1827.

Informal definition

Saddle surface with normal planes in directions of principal curvatures

At any point on a surface, we can find a normal vector that is at right angles to the surface; planes containing the normal vector are called normal planes. The intersection of a normal plane and the surface will form a curve called a normal section and the curvature of this curve is the normal curvature. For most points on most surfaces, different normal sections will have different curvatures; the maximum and minimum values of these are called the principal curvatures, call these κ1, κ2. The Gaussian curvature is the product of the two principal curvatures Κ = κ1κ2.

The sign of the Gaussian curvature can be used to characterise the surface.

If both principal curvatures are of the same sign: κ1κ2 > 0, then the Gaussian curvature is positive and the surface is said to have an elliptic point. At such points, the surface will be dome like, locally lying on one side of its tangent plane. All sectional curvatures will have the same sign.
If the principal curvatures have different signs: κ1κ2 < 0, then the Gaussian curvature is negative and the surface is said to have a hyperbolic or saddle point. At such points, the surface will be saddle shaped. Because one principal curvature is negative, one is positive, and the normal curvature varies continuously if you rotate a plane orthogonal to the surface around the normal to the surface in two directions, the normal curvatures will be zero giving the asymptotic curves for that point.
If one of the principal curvatures is zero: κ1κ2 = 0, the Gaussian curvature is zero and the surface is said to have a parabolic point.

Most surfaces will contain regions of positive Gaussian curvature (elliptical points) and regions of negative Gaussian curvature separated by a curve of points with zero Gaussian curvature called a parabolic line.
Relation to geometries

When a surface has a constant zero Gaussian curvature, then it is a developable surface and the geometry of the surface is Euclidean geometry.

When a surface has a constant positive Gaussian curvature, then it is a sphere and the geometry of the surface is spherical geometry.

When a surface has a constant negative Gaussian curvature, then it is a pseudospherical surface and the geometry of the surface is hyperbolic geometry.

Relation to principal curvatures

The two principal curvatures at a given point of a surface are the eigenvalues of the shape operator at the point. They measure how the surface bends by different amounts in different directions at that point. We represent the surface by the implicit function theorem as the graph of a function, f, of two variables, in such a way that the point p is a critical point, that is, the gradient of f vanishes (this can always be attained by a suitable rigid motion). Then the Gaussian curvature of the surface at p is the determinant of the Hessian matrix of f (being the product of the eigenvalues of the Hessian). (Recall that the Hessian is the 2×2 matrix of second derivatives.) This definition allows one immediately to grasp the distinction between a cup/cap versus a saddle point.

Alternative definitions

It is also given by

\( {\displaystyle K={\frac {{\bigl \langle }(\nabla _{2}\nabla _{1}-\nabla _{1}\nabla _{2})\mathbf {e} _{1},\mathbf {e} _{2}{\bigr \rangle }}{\det g}},} \)

where ∇i = ∇ei is the covariant derivative and g is the metric tensor.

At a point p on a regular surface in R3, the Gaussian curvature is also given by

\( {\displaystyle K(\mathbf {p} )=\det S(\mathbf {p} ),} \)

where S is the shape operator.

A useful formula for the Gaussian curvature is Liouville's equation in terms of the Laplacian in isothermal coordinates.

Total curvature

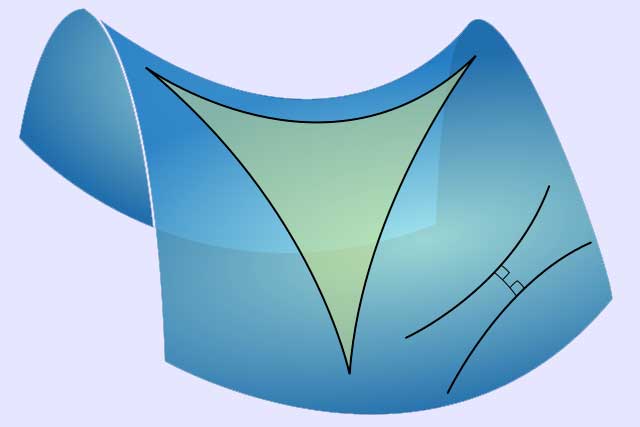
The sum of the angles of a triangle on a surface of negative curvature is less than that of a plane triangle.

The surface integral of the Gaussian curvature over some region of a surface is called the total curvature. The total curvature of a geodesic triangle equals the deviation of the sum of its angles from π. The sum of the angles of a triangle on a surface of positive curvature will exceed π, while the sum of the angles of a triangle on a surface of negative curvature will be less than π. On a surface of zero curvature, such as the Euclidean plane, the angles will sum to precisely π radians.

\( \sum _{i=1}^{3}\theta _{i}=\pi +\iint _{T}K\,dA. \)

A more general result is the Gauss–Bonnet theorem.
Important theorems

Theorema egregium
Main article: Theorema egregium

Gauss's Theorema egregium (Latin: "remarkable theorem") states that Gaussian curvature of a surface can be determined from the measurements of length on the surface itself. In fact, it can be found given the full knowledge of the first fundamental form and expressed via the first fundamental form and its partial derivatives of first and second order. Equivalently, the determinant of the second fundamental form of a surface in R³ can be so expressed. The "remarkable", and surprising, feature of this theorem is that although the definition of the Gaussian curvature of a surface S in R³ certainly depends on the way in which the surface is located in space, the end result, the Gaussian curvature itself, is determined by the intrinsic metric of the surface without any further reference to the ambient space: it is an intrinsic invariant. In particular, the Gaussian curvature is invariant under isometric deformations of the surface.

In contemporary differential geometry, a "surface", viewed abstractly, is a two-dimensional differentiable manifold. To connect this point of view with the classical theory of surfaces, such an abstract surface is embedded into R³ and endowed with the Riemannian metric given by the first fundamental form. Suppose that the image of the embedding is a surface S in R³. A local isometry is a diffeomorphism f : U → V between open regions of R³ whose restriction to S ∩ U is an isometry onto its image. Theorema egregium is then stated as follows:

The Gaussian curvature of an embedded smooth surface in R3 is invariant under the local isometries.

For example, the Gaussian curvature of a cylindrical tube is zero, the same as for the "unrolled" tube (which is flat).[1] On the other hand, since a sphere of radius R has constant positive curvature R-2 and a flat plane has constant curvature 0, these two surfaces are not isometric, even locally. Thus any planar representation of even a part of a sphere must distort the distances. Therefore, no cartographic projection is perfect.

Gauss–Bonnet theorem
Main article: Gauss–Bonnet theorem

The Gauss–Bonnet theorem links the total curvature of a surface to its Euler characteristic and provides an important link between local geometric properties and global topological properties.
Surfaces of constant curvature

Minding's theorem (1839) states that all surfaces with the same constant curvature K are locally isometric. A consequence of Minding's theorem is that any surface whose curvature is identically zero can be constructed by bending some plane region. Such surfaces are called developable surfaces. Minding also raised the question of whether a closed surface with constant positive curvature is necessarily rigid.
Liebmann's theorem (1900) answered Minding's question. The only regular (of class C2) closed surfaces in R3 with constant positive Gaussian curvature are spheres.[2] If a sphere is deformed, it does not remain a sphere, proving that a sphere is rigid. A standard proof uses Hilbert's lemma that non-umbilical points of extreme principal curvature have non-positive Gaussian curvature.[3]
Hilbert's theorem (1901) states that there exists no complete analytic (class Cω) regular surface in R3 of constant negative Gaussian curvature. In fact, the conclusion also holds for surfaces of class C2 immersed in R3, but breaks down for C1-surfaces. The pseudosphere has constant negative Gaussian curvature except at its singular cusp.[4]

Alternative formulas

Gaussian curvature of a surface in R3 can be expressed as the ratio of the determinants of the second and first fundamental forms II and I:

\( {\displaystyle K={\frac {\det(\mathrm {I\!I} )}{\det(\mathrm {I} )}}={\frac {LN-M^{2}}{EG-F^{2}}}.} \)

The Brioschi formula gives Gaussian curvature solely in terms of the first fundamental form:

\( {\displaystyle K={\frac {{\begin{vmatrix}-{\frac {1}{2}}E_{vv}+F_{uv}-{\frac {1}{2}}G_{uu}&{\frac {1}{2}} E_{u}&F_{u}-{\frac {1}{2}}E_{v}\\F_{v}-{\frac {1}{2}}G_{u}&E&F\\{\frac {1}{2}}G_{v}&F&G\end{vmatrix}}-{\begin{vmatrix}0&{\frac {1}{2}}E_{v}&{\frac {1}{2}}G_{u}\\{\frac {1}{2}}E_{v}&E&F\\{\frac {1}{2}}G_{u}&F&G\end{vmatrix}}}{\left(EG-F^{2}\right)^{2}}}} \)

For an orthogonal parametrization (F = 0), Gaussian curvature is:

\( K=-{\frac {1}{2{\sqrt {EG}}}}\left({\frac {\partial }{\partial u}}{\frac {G_{u}}{\sqrt {EG}}}+ {\frac {\partial }{\partial v}}{\frac {E_{v}}{\sqrt {EG}}}\right). \)

For a surface described as graph of a function z = F(x,y), Gaussian curvature is:

\( {\displaystyle K={\frac {F_{xx}\cdot F_{yy}-F_{xy}^{2}}{\left(1+F_{x}^{2}+F_{y}^{2}\right)^{2}}}} \)

For an implicitly defined surface, F(x,y,z) = 0, the Gaussian curvature can be expressed in terms of the gradient ∇F and Hessian matrix H(F):[5][6]

\( {\displaystyle K=-{\frac {\begin{vmatrix}H(F)&\nabla F^{\mathsf {T}}\\\nabla F&0\end{vmatrix}} {|\nabla F|^{4}}}=-{\frac {\begin{vmatrix}F_{xx}&F_{xy}&F_{xz}&F_{x}\\F_{xy}&F_{yy}&F_{yz}&F_{y} \\F_{xz}&F_{yz}&F_{zz}&F_{z}\\F_{x}&F_{y}&F_{z}&0\\\end{vmatrix}} {|\nabla F|^{4}}}} \)

For a surface with metric conformal to the Euclidean one, so F = 0 and E = G = eσ, the Gauss curvature is given by (Δ being the usual Laplace operator):

\( {\displaystyle K=-{\frac {1}{2e^{\sigma }}}\Delta \sigma .} \)

Gaussian curvature is the limiting difference between the circumference of a geodesic circle and a circle in the plane:[7]

\( K=\lim _{r\to 0^{+}}3{\frac {2\pi r-C(r)}{\pi r^{3}}} \)

Gaussian curvature is the limiting difference between the area of a geodesic disk and a disk in the plane:[7]

\( {\displaystyle K=\lim _{r\to 0^{+}}12{\frac {\pi r^{2}-A(r)}{\pi r^{4}}}}

Gaussian curvature may be expressed with the Christoffel symbols:[8]

\( K=-{\frac {1}{E}}\left({\frac {\partial }{\partial u}}\Gamma _{12}^{2}-{\frac {\partial }{\partial v}}\Gamma _{11}^{2}+\Gamma _{12}^{1}\Gamma _{11}^{2}-\Gamma _{11}^{1}\Gamma _{12}^{2}+\Gamma _{12}^{2}\Gamma _{12}^{2}-\Gamma _{11}^{2}\Gamma _{22}^{2}\right) \)