In mathematics and computational geometry, the Gabriel graph of a set S of points in the Euclidean plane expresses one notion of proximity or nearness of those points. Formally, it is the graph G with vertex set S in which any points \( p\in S \) and \( {\displaystyle q\in S} \) are adjacent precisely if they are distinct, i.e. \( p \neq q \), and the closed disc of which line segment \( {\displaystyle {\overline {pq}}} \) is a diameter contains no other elements of S. Gabriel graphs naturally generalize to higher dimensions, with the empty disks replaced by empty closed balls. Gabriel graphs are named after K. Ruben Gabriel, who introduced them in a paper with Robert R. Sokal in 1969.
The Gabriel graph of 100 random points
Percolation
A finite site percolation threshold for Gabriel graphs has been proven to exist by Bertin, Billiot & Drouilhet (2002), and more precise values of both site and bond thresholds have been given by Norrenbrock (2014).
Related geometric graphs
The Gabriel graph is a subgraph of the Delaunay triangulation. It can be found in linear time if the Delaunay triangulation is given (Matula & Sokal 1980).
The Gabriel graph contains, as subgraphs, the Euclidean minimum spanning tree, the relative neighborhood graph, and the nearest neighbor graph.
It is an instance of a beta-skeleton. Like beta-skeletons, and unlike Delaunay triangulations, it is not a geometric spanner: for some point sets, distances within the Gabriel graph can be much larger than the Euclidean distances between points (Bose et al. 2006).
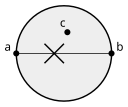
Points a and b are Gabriel neighbours, as c is outside their diameter circle.
The presence of point c within the circle prevents points a and } b from being Gabriel neighbors.
References
Bertin, Etienne; Billiot, Jean-Michel; Drouilhet, Rémy (2002), "Continuum percolation in the Gabriel graph", Advances in Applied Probability, 34 (4): 689–701, doi:10.1239/aap/1037990948, MR 1938937.
Bose, Prosenjit; Devroye, Luc; Evans, William; Kirkpatrick, David (2006), "On the spanning ratio of Gabriel graphs and β-skeletons", SIAM Journal on Discrete Mathematics, 20 (2): 412–427, CiteSeerX 10.1.1.46.4728, doi:10.1137/S0895480197318088, MR 2257270.
Gabriel, Kuno Ruben; Sokal, Robert Reuven (1969), "A new statistical approach to geographic variation analysis", Systematic Biology, Society of Systematic Biologists, 18 (3): 259–278, doi:10.2307/2412323, JSTOR 2412323.
Matula, David W.; Sokal, Robert Reuven (1980), "Properties of Gabriel graphs relevant to geographic variation research and clustering of points in the plane", Geogr. Anal., 12 (3): 205–222, doi:10.1111/j.1538-4632.1980.tb00031.x.
Norrenbrock, Christoph (2014), Percolation threshold on planar Euclidean Gabriel Graphs, arXiv:1406.0663, Bibcode:2014arXiv1406.0663N.
Undergraduate Texts in Mathematics
Graduate Studies in Mathematics
Hellenica World - Scientific Library
Retrieved from "http://en.wikipedia.org/"
All text is available under the terms of the GNU Free Documentation License