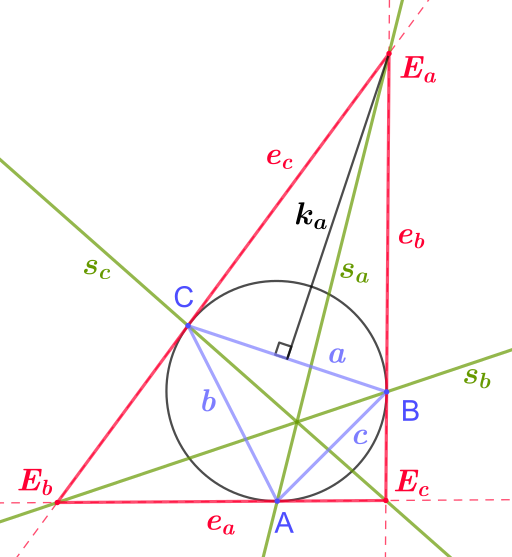
The exsymmedians are three lines associated with a triangle. More precisely for a given triangle the exsymmedians are the tangent lines on the triangle's circumcircle through the three vertices of the triangle. The triangle formed by the three exsymmedians is the tangential triangle and its vertices, that is the three intersections of the exsymmedians are called exsymmedian points.
For a triangle ABC with \( {\displaystyle e_{a},e_{b},e_{c}} \( being the exsymmedians and \( {\displaystyle s_{a},s_{b},s_{c}} \) being the symmedians through the vertices A,B,C two exsymmedians and one symmedian intersect in a common point, that is:
\( {\displaystyle {\begin{aligned}E_{a}&=e_{b}\cap e_{c}\cap s_{a}\\E_{b}&=e_{a}\cap e_{c}\cap s_{b}\\E_{c}&=e_{a}\cap e_{b}\cap s_{c}\end{aligned}}}} \)
The length of the perpendicular line segment connecting a triangle side with its associated exsymmedian point is proportional to that triangle side. Specifically the following formulas apply:
\( {\displaystyle {\begin{aligned}k_{a}&=a\cdot {\frac {2\triangle }{c^{2}+b^{2}-a^{2}}}\\[6pt]k_{b}&=b\cdot {\frac {2\triangle }{c^{2}+a^{2}-b^{2}}}\\[6pt]k_{c}&=c\cdot {\frac {2\triangle }{a^{2}+b^{2}-c^{2}}}\end{aligned}}}} \)
Here \( \triangle \) denotes the area of the triangle ABC and \( {\displaystyle k_{a},k_{b},k_{c}} \) the perpendicular line segments connecting the triangle sides a,b,c with the exsymmedian points \( {\displaystyle E_{a},E_{b},E_{c}} \).
References
Roger A. Johnson: Advanced Euclidean Geometry. Dover 2007, ISBN 978-0-486-46237-0, pp. 214–215 (originally published 1929 with Houghton Mifflin Company (Boston) as Modern Geometry).
Undergraduate Texts in Mathematics
Graduate Studies in Mathematics
Hellenica World - Scientific Library
Retrieved from "http://en.wikipedia.org/"
All text is available under the terms of the GNU Free Documentation License