.
Στην αστρονομία, ο όρος υπερφωτεινή κίνηση αναφέρεται στη φαινομενική ικανότητα κάποιων αντικειμένων να κινούνται με ταχύτητες μεγαλύτερες από εκείνη του φωτός στο κενό (ήτοι ≈ 3 × 108 m/s). Το φαινόμενο της υπερφωτεινής κίνησης έχει παρατηρηθεί σε ουράνια αντικείμενα όπως είναι οι ραδιογαλαξίες, τα κβάζαρ και πρόσφατα ακόμα και σε μικροκβάζαρ.
Το φαινόμενο της υπερφωτεινής κίνησης είναι ευρέως αποδεκτό ότι οφείλεται σε ψευδαίσθηση και όχι σε παραβίαση της ειδικής θεωρίας της σχετικότητας (ΕΘΣ), σύμφωνα με την οποία η μέγιστη ταχύτητα με την οποία μπορεί να μεταδοθεί πληροφορία είναι η ταχύτητα του φωτός.
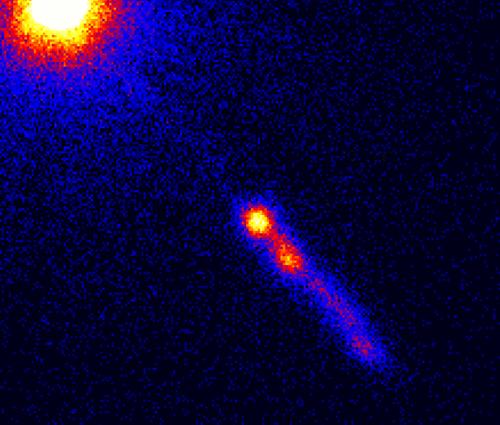
Φωτογραφία από το διαστημικό τηλεσκόπιο Chandra στις ακτίνες Χ του ΕΓΠ 3C 273 και του αντίστοιχου πίδακά του, στον οποίο παρατηρείται υπερφωτεινή κίνηση.
Ιστορικό
Το ιστορικό της παρατήρησης υπερφωτεινής κίνησης σε ενεργούς γαλαξίες ξεκινάει στις αρχές της δεκαετίας του 70' από παρατηρήσεις κβάζαρ στην περιοχή των ραδιοκυμάτων και τις συνακόλουθες εργασίες των Knight et al. (1971)[1] και Whitney et al. (1971).[2] Οι εργασίες αυτές ανέδειξαν λεπτές δομές στο ραδιοφωνικό φάσμα των κβάζαρ 3C 273 και 3C 279. Συγκεκριμένα, οι δύο ομάδες ανακάλυψαν μία διπλή, συμμετρική πηγή ραδιοφωνικών κυμάτων στο κβάζαρ 3C 279 της οποίας το γωνιακό μέγεθος αυξήθηκε μεταξύ των παρατηρήσεων των δύο προαναφερθέντων άρθρων από (1.55 ± 0.03) × 10-3 arcsec σε (1.69 ± 0.02) × 10-3 arcsec. Δεδομένης της απόστασης στην οποία αντιστοιχεί η ερυθρή μετατόπιση που παρουσιάζει το 3C 279 (z=0.538), ο γωνιακή μετατόπιση μεταξύ των δύο πηγών ραδιοκυμάτων μεταφράζεται σε μία φυσική μετατόπιση με ταχύτητα ≈ 10c. Την ίδια χρονιά η ομάδα των Cohen et al. παρατήρησαν επίσης υπερφωτεινή κίνηση (ή «υπερφωτεινή διαστολή» (superlight expansion) όπως αναφέρεται το φαινόμενο στην εργασία τους) στα κβάζαρ 3C 279 και 3C 273.[3]
Τόσο η ομάδα των Whitney et al. όσο και εκείνη των Cohen et al. πρότειναν διάφορους τρόπους για να ερμηνευθεί η παρατηρούμενη υπερφωτεινή κίνηση στα δύο αυτά κβάζαρ. Ένα από τα μοντέλα που πρότειναν είναι το λεγόμενο «μοντέλο του χριστουγεννιάτικου δέντρου» (Christmas tree model) —σύμφωνα με το οποίο ορισμένες από τις πηγές ραδιοκυμάτων των προαναφερθέντων κβάζαρ αναβοσβήνουν— και μη κοσμολογικές ερυθρές μετατοπίσεις. Σύντομα όμως η αστρονομική κοινότητα άρχισε να αποδέχεται την σημερινά αποδεκτή εξήγηση του Rees, ο οποίος είχε ήδη προβλέψει από το 1966 τη φαινομενική υπερφωτεινή κίνηση ραδιοφωνικών πηγών λόγω σχετικιστικών φαινομένων.[4]
Από τότε άρχισε να αναδύεται μία καινούρια εικόνα όσον αφορά την παρατηρούμενη υπερφωτεινή κίνηση ραδιοφωνικών πηγών στους πίδακες ορισμένων κβάζαρ και ραδιογαλαξιών. Η εικόνα αυτή βασίζεται στην υπόθεση ότι από τις κεντρικές περιοχές των αντικειμένων αυτών εκτοξεύονται ανά τακτά χρονικά διαστήματα (της τάξης των μερικών ετών) νέφη αέριων μαζών κατά μήκος ενός [λίγο-πολύ] σταθερού άξονα. Το μοντέλο αυτό είναι σε θέση να εξηγήσει επίσης την παρατηρούμενη μεταβολή στο ραδιοφωνικό φάσμα γαλαξιακών πυρήνων, όπως έδειξαν οι Blandford και Konigl το 1979.[5] Σύμφωνα με το μοντέλο τους, οι προαναφερθείσες μεταβολές οφείλονται στις διαταραχές που προκαλεί η τακτική εκτόξευση νεφών ύλης κατά μήκος ενός σχετικιστικού πίδακα που παρατηρείται υπό μικρή γωνία και προέρχεται από τα κέντρα των αντικειμένων αυτών.
Το φαινόμενο της υπερφωτεινής κίνησης έχει παρατηρηθεί μέχρι σήμερα σε πολλά κβάζαρ και ραδιογαλαξίες.[6] Ένα πιθανώς ανάλογο φαινόμενο έχει παρατηρηθεί επίσης σε συστήματα μελανών οπών στον Γαλαξία.[7]
Θεωρητική εξήγηση
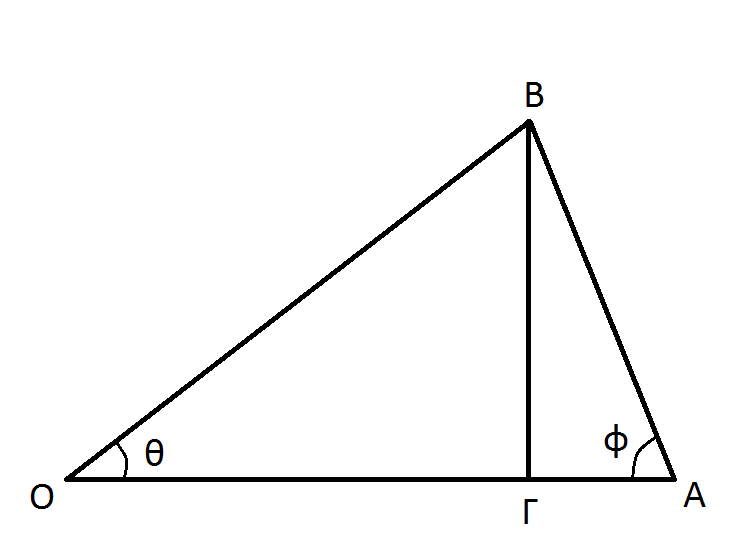
Γεωμετρία διάταξης στην οποία ένας παρατηρητής στη θέση Ο παρατηρεί ένα νέφος σχετικιστικής ύλης να κινείται από το σημείο Α στο σημείο Β.
Σύμφωνα με το μοντέλο του Rees (1966), οι μετρούμενες υπερφωτεινές κινήσεις οφείλονται σε ψευδαίσθηση και όχι σε παραβίαση της ΕΘΣ του Αϊνστάιν. Αντιθέτως, η ύπαρξη φαινομενικών υπερφωτεινών κινήσεων είναι αναμενόμενη από τη θεωρία υποθέτοντας ότι οι ενεργοί γαλαξιακοί πυρήνες από τους οποίους παρατηρούνται τέτοια φαινόμενα εκτοξεύουν σχετικιστικά κινούμενα σωματίδια που εκπέμπουν φωτεινά σήματα υπό μικρή γωνία σε σχέση με τον ορίζοντα παρατήρησης. Στα πλαίσια του παραπάνω μοντέλου, είναι δυνατόν να δειχθεί ότι η φαινόμενη ταχύτητα, vapp αυτών των σωματιδίων είναι[8]
\begin{align} v_{\textrm{app}}=\frac{(v/c)\sin{\phi}}{1-(v/c)\cos{\phi}}\, \quad (1) \end{align}
όπου φ η γωνία παρατήρησης (βλέπε σχετικό σχήμα στα δεξιά) και v η πραγματική σχετική ταχύτητα των σωμάτων.
Απόδειξη[Σημ. 1]
Έστω αδρανειακός παρατηρητής που βρίσκεται στη θέση Ο και παρατηρεί μία πηγή (νέφος) ραδιοκυμάτων που εκτοξεύθηκε από το κέντρο ενός κβάζαρ/ραδιογαλαξία να μετακινείται από το σημείο Α στο σημείο Β (βλέπε διπλανό σχήμα). Έστω επίσης ότι το νέφος αυτό κινείται με ταχύτητα v, η οποία είναι μικρότερη της ταχύτητας του φωτός, όπως υπαγορεύει η Ειδική Σχετικότητα.
Αν η γωνία παρατήρησης θ είναι μικρή, τότε είναι φανερό από βασική τριγωνομετρία ότι θα ισχύει η παρακάτω σχέση:
\cos{\theta}=\frac{\Omicron\Gamma}{\Omicron\Beta} \ \xrightarrow{\theta\ll 1}\ \Omicron\Gamma\approx\Omicron\Beta
Ο τρόπος με τον οποίο υπολογίζεται η ταχύτητα μίας τέτοιας πηγής σε πίδακες ενεργών γαλαξιών είναι παίρνοντας εικόνες του στα ραδιοφωνικά μήκη κύματος και παρατηρώντας πώς η πηγή αυτή κινείται σε δεδομένο χρονικό διάστημα μεταξύ δύο παρατηρήσεων. Γνωρίζοντας την απόσταση μεταξύ των δύο σημείων στη φωτογραφία είναι δυνατόν να υπολογιστεί η ταχύτητα διαιρώντας την απόσταση αυτή με το αντίστοιχο χρονικό διάστημα που παρήλθε κατά την κίνηση μεταξύ των δύο αυτών σημείων. Αξίζει να σημειωθεί ότι η απόσταση που μετράται σε μία φωτογραφία ισούται με την εγκάρσια απόσταση που διήνυσε η πηγή ως προς τον ορίζοντα παρατήρησης. Εν προκειμένω, η εγκάρσια απόσταση ισούται με ΒΓ.
Αν δt' λοιπόν το χρονικό διάστημα που χρειάζεται το νέφος ώστε να φτάσει από το σημείο Α στο σημείο Β ως προς τον παρατηρητή που βρίσκεται στο σημείο Ο και D η εγκάρσια απόσταση ΒΓ που διήνυσε το νέφος, τότε η φαινόμενη ταχύτητα, vapp, του νέφους που μετρά ο Ο είναι
\begin{align} v_{\textrm{app}}=\frac{D}{\delta t'} \end{align}
Για να συγκρίνουμε με κάποιο τρόπο τη φαινόμενη ταχύτητα του νέφους με την πραγματική, πρέπει να συνδέσουμε τις ποσότητες D και δt' με την πραγματική ταχύτητα του νέφους. Όμως, η απόσταση D ισούται με το γινόμενο της εγκάρσιας συνιστώσας της ταχύτητας του νέφους, vsinφ, επί το χρονικό διάστημα δt που χρειάζεται το νέφος για να διασχίσει την απόσταση ΑΒ ως προς το σύστημα ηρεμίας του. Συνεπώς,
D=(v\sin{\phi})\delta t \ \ \
Έστω ότι τη χρονική στιγμή tA το νέφος βρίσκεται στο σημείο Α και εκπέμπει ένα φωτεινό σήμα υπό τη μορφή ραδιοκυμάτων. Αφού το σήμα αυτό κινείται με ταχύτητα c, ο παρατηρητής που βρίσκεται στο σημείο Ο θα λάβει το σήμα αυτό μετά από χρόνο
\( t'_{\Alpha}=t_{\Alpha}+\frac{\Omicron\Alpha}{c}=t_{\Alpha}+\frac{\Omicron\Gamma}{c}+\frac{\Gamma\Alpha}{c}
\)
Αντίστοιχα, αν τη χρονική στιγμή tΒ το νέφος στείλει ένα φωτεινό σήμα από το σημείο Β, τότε ο παρατηρητής στο σημείο Ο θα το λάβει μετά από χρόνο
t'_{\Beta}=t_{\Beta}+\frac{\Omicron\Beta}{c}
Σύμφωνα λοιπόν με τον παρατηρητή Ο, το νέφος διανύει την απόσταση ΑΒ σε χρονικό διάστημα
\delta t'=t'_{\Beta}-t'_{\Alpha}=t_{\Beta}+\frac{\Omicron\Beta}{c}-t_{\Alpha}-\frac{\Omicron\Gamma}{c}-\frac{\Gamma\Alpha}{c}
Όμως, η διαφορά tΒ-tΑ αντιστοιχεί στο χρονικό διάστημα δt όπως αυτό είχε ορισθεί παραπάνω. Επίσης, για μικρή γωνία παρατήρησης θ ισχύει η προσέγγιση ΟΓ≈ΟΒ. Συνεπώς, η σχέση μεταξύ των χρονικών διαστημάτων δt και δt' είναι:
\delta t'=\delta t-\frac{\Gamma\Alpha}{c}\ \xrightarrow{\Gamma\Alpha=(v\cos{\phi})\delta t}\ \delta t'=\delta t\left(1-\frac{v\cos{\phi}}{c}\right)
Άρα λοιπόν, η φαινόμενη ταχύτητα του νέφους ως προς τον παρατηρητή Ο είναι
\begin{align} \beta_{\textrm{app}}=\frac{\beta\sin{\phi}}{1-\beta\cos{\phi}} \end{align}
όπου β=v/c και βapp=vapp/c.
Όπως μπορεί να δειχθεί, η μέγιστη τιμή που μπορεί να πάρει η φαινόμενη ταχύτητα σύμφωνα σχέση (1) και η αντίστοιχη γωνία στην οποία συμβαίνει αυτό είναι:
\begin{align} & v_{\textrm{app}}^{\textrm{max}}=\gamma v \\ & \cos\phi_{\textrm{max}}=\frac{v}{c} \end{align}
όπου γ=(1-β2)-1/2 ο παράγοντας Λόρεντζ. Επειδή ο παράγοντας Λόρεντζ μπορεί, θεωρητικά, να πάρει οποιαδήποτε τιμή μεγαλύτερη της μονάδας, είναι φανερό ότι βάσει του παραπάνω μοντέλου η φαινόμενη ταχύτητα μίας σχετικιστικά κινούμενης φωτεινής πηγής που παρατηρείται υπό μικρή γωνία μπορεί πράγματι να είναι μεγαλύτερη από την ταχύτητα του φωτός.
Παρόμοιοι υπολογισμοί μπορούν επίσης να προσδιορίσουν την ελάχιστη πραγματική σχετική ταχύτητα, vmin, και γωνία παρατήρησης, φmin:[9]
\begin{align} & \frac{v_{\textrm{min}}}{c}=\sqrt{\frac{(v_{\textrm{app}}/c)^2}{1+(v_{\textrm{app}}/c)^2}} \\ & \cot\phi_{\textrm{min}}=\frac{v_{\textrm{app}}}{c} \end{align}
Εφαρμογή 1 − Το κβάζαρ 3C 279
Όπως έδειξαν οι Whitney et al. (1971), το ραδιοφωνικό φάσμα του κβάζαρ 3C 279 παρουσιάζει μία διπλή, συμμετρική πηγή της οποίας το γωνιακό μέγεθος αυξάνεται με ρυθμό ο οποίος, σε συνδυασμό με την απόσταση που αντιστοιχεί στην μετρούμενη ερυθρή μετατόπιση του αντικειμένου, υπονοεί υπερφωτεινή κίνηση ταχύτητας ≈ 10c. Αν δεχτούμε το σημερινά αποδεκτό μοντέλο του Rees (1966), τότε η ταχύτητα αυτή αντιστοιχεί στην φαινόμενη ταχύτητα, vapp, όπως αυτή ορίσθηκε στην παραπάνω ανάλυση. Αν τώρα υποθέσουμε ότι ο άξονας του (υποτιθέμενου) πίδακα του 3C 279 σχηματίζει τέτοια γωνία ώστε η φαινόμενη ταχύτητα να παίρνει τη μέγιστη δυνατή τιμή της (cosφ=β), τότε μπορούμε να λύσουμε τη σχέση vappmax=γv ως προς την πραγματική ταχύτητα με την οποία διαστέλλεται η διπλή πηγή στο εν λόγω κβάζαρ και να κάνουμε την αντικατάσταση vappmax=10c:
\beta=\frac{\beta_{\textrm{app}}^{\textrm{max}}}{\sqrt{1+(\beta_{\textrm{app}}^{\textrm{max}})^2}}\ \xrightarrow{\beta_{\textrm{app}}^{\textrm{max}}=10}\ v\approx 0.995 c
που είναι, όπως απαιτεί η Ειδική Σχετικότητα, μικρότερη από την ταχύτητα του φωτός. Γνωρίζοντας όμως ποια θα πρέπει να είναι η πραγματική ταχύτητα διαστολής της διπλής πηγής, μπορούμε επίσης να υπολογίσουμε την γωνία που θα πρέπει να σχηματίζει ο άξονας του πίδακα με την ευθεία παρατήρησης. Συγκεκριμένα,
\cos{\phi}=\beta\ \xrightarrow{\beta\approx0.995}\ \phi\approx5.7^{\circ}
Εφαρμογή 2 - Το κβάζαρ 3C 273[Σημ. 2]
Ένα νέφος-ραδιοπηγή παρατηρείται ότι εκτοξεύτηκε από τον πυρήνα του κβάζαρ 3C 273 και κινείται με γωνιακή ταχύτητα 0.0008” (δευτερόλεπτα τόξου) ανά έτος. Για το παρατηρούμενο κοσμολογικό redshift του κβάζαρ και τα δεδομένα του WMAP για την σταθερά του Χαμπλ, η ταχύτητα αυτή αντιστοιχεί σε φαινόμενη ταχύτητα ίση με 7.85c.[10]
Για να είναι η παρατήρηση σύμφωνη με το μοντέλο των σχετικιστικά κινούμενων ραδιοπηγών, η ελάχιστη γωνία παρατήρησης του νέφους που παρατηρείται στο 3C 273 πρέπει να είναι
\begin{align} \phi_{\textrm{min}}=\cot^{-1}\left(\frac{v_{\textrm{app}}}{c}\right)\approx7.26^{\circ} \end{align}
Η αντίστοιχη ελάχιστη πραγματική σχετική ταχύτητα του νέφους πρέπει αντίστοιχα να είναι
\begin{align} v_{\textrm{min}}=c\,\sqrt{\frac{(v_{\textrm{app}}/c)^2}{1+(v_{\textrm{app}}/c)^2}}\approx 0.992c \end{align}
Περαιτέρω ενδείξεις για το μοντέλο των σχετικιστικών πιδάκων
Το μοντέλο των σχετικιστικών πιδάκων δεν έγινε αμέσως αποδεκτό από την αστρονομική κοινότητα. Αντιθέτως, άρχισε σταδιακά να γίνεται αποδεκτό αφενός μεν λόγω των συσσωρευμένων παρατηρησιακών δεδομένων που συναινούν υπέρ του εν λόγω μοντέλου, καθώς επίσης και από το γεγονός ότι, από όλα τα μοντέλα που έχουν προταθεί, είναι σε θέση να εξηγήσει αρκετά από τα διάφορα φαινομένα που σχετίζονται με την παρατηρούμενη υπερφωτεινή κίνηση στα κβάζαρ και στους γαλαξίες. Επιπροσθέτως, το μοντέλο αυτό βασίζεται στις λιγότερες δυνατές υποθέσεις και βρίσκεται σε συμφωνία με άλλα ευρέως αποδεκτά φαινόμενα (όπως για παράδειγμα η κοσμολογική φύση των παρατηρούμενων ερυθρών μετατοπίσεων των ενεργών γαλαξιών στους οποίους παρατηρούνται τέτοια εξωτικά φαινόμενα).
Ορισμένες από τις ισχυρότερες ενδείξεις υπέρ του σημερινά αποδεκτού μοντέλου είναι το γεγονός ότι σχεδόν όλοι οι ΕΓΠ στους οποίους παρατηρούνται υπερφωτεινές κινήσεις περιτριγυρίζονται από εκτεταμένες άλω που μπορεί να είναι ραδιολοβοί που είναι προσανατολισμένοι κατά τον ορίζοντα παρατήρησης. Επιπροσθέτως, το μοντέλο είναι σε θέση να εξηγήσει τις απότομες μεταβολές στις λαμπρότητες των ΕΓΠ, καθώς βάσει αυτού οποιαδήποτε χρονική μεταβολή της λαμπρότητας θα παρατηρείται από τους αστρονόμους στη Γη κατά [περίπου] 2γ (όπου γ ο παράγοντας Λόρεντζ) φορές συντομότερη. Τέλος, μία ακόμα σημαντική επιτυχία του μοντέλου είναι ότι εξηγεί φυσιολογικά το παρατηρησιακό γεγονός ότι οι υποτιθέμενοι πίδακες σχετικιστικής ύλης είναι μονομερείς (δηλαδή το γεγονός ότι βλέπουμε μόνο τη μία μεριά του πίδακα), καθώς λόγω της σχετικιστικής κίνησης τα ραδιοκύματα που εκπέμπουν τα σωμάτια του πίδακα λόγω του λεγόμενου «φαινομένου του προβολέα» (αγγλικά: headlight effect) είναι αναμενόμενο ότι η ακτινοβολία που προέρχεται από την πλευρά του πίδακα που βρίσκεται αντιδιαμετρικά του άξονα παρατήρησης θα φαίνεται να είναι εξαιρετικά αμυδρή.[11]
Σημειώσεις
Δείτε σχετική συζήτηση στο βιβλίο των Carroll & Ostlie "An Introduction to Modern Astrophysics", σελ. 1127
Δείτε τις σχετικές ασκήσεις 28.3.3 και 28.3.4 στο βιβλίο των Carroll & Ostlie "An Introduction to Modern Astrophysics", σελ. 1126 και 1128
Παραπομπές
Knight, Curtis A.; Robertson, Douglas S.; Rogers, Alan E. E.; Shapiro, Irwin I.; Whitney, Alan R.; Clark, Thomas A.; Goldstein, Richard M.; Marandino, Gerard E.; Vandenberg, Nancy R. (1971). «Quasars: Millisecond-of-Arc Structure Revealed by Very-Long-Baseline Interferometry». Science 172 (3978): 52-54. doi:10.1126/science.172.3978.52. Bibcode: 1971Sci...172...52K.
Whitney, Alan R.; Shapiro, Irwin I.; Rogers, Alan E. E.; Robertson, Douglas S.; Knight, Curtis A.; Clark, Thomas A.; Goldstein, Richard M.; Marandino, Gerard E.; Vandenberg, Nancy R. (1971). «Quasars Revisited: Rapid Time Variations Observed Via Very-Long-Baseline Interferometry». Science 173 (3993): 225-230. doi:10.1126/science.173.3993.225. Bibcode: 1971Sci...173..225W.
Cohen, M. H.; Cannon, W.; Purcell, G. H.; Shaffer, D. B.; Broderick, J. J.; Kellermann, K. I.; Jauncey, D. L. (1971). «The Small-Scale Structure of Radio Galaxies and Quasi-Stellar Sources at 3.8 Centimeters». ApJ 170: 270. doi:10.1086/151204. Bibcode: 1971ApJ...170..207C.
Rees, M. J. (1966). «Appearance of Relativistically Expanding Radio Sources». Nature 211 (5048): 468-470. doi:10.1038/211468a0. Bibcode: 1966Natur.211..468R.
Blandford, R. D.; Konigl, A. (1979). «Relativistic jets as compact radio sources». ApJ 232: 34-38. doi:10.1086/157262. Bibcode: 1979ApJ...232...34B.
Zhang, Yong-Wei; Fan, Jun-Hui (2008). «Statistics of Superluminal Motion in Active Galactic Nuclei». Chinese Journal of Astronomy and Astrophysics 8 (4): 385-394. doi:10.1088/1009-9271/8/4/02. Bibcode: 2008ChJAA...8..385Z.
Mirabel, I. F.; Rodríguez, L. F. (1994). «A superluminal source in the Galaxy». Nature 371 (6492): 46-48. doi:10.1038/371046a0. Bibcode: 1994Natur.371...46M.
Carroll & Ostlie. An Introduction to Modern Astrophysics, σελ. 1127.
Carroll & Ostlie. An Introduction to Modern Astrophysics, σελ. 1128.
Carroll & Ostlie. An Introduction to Modern Astrophysics, σελ. 1126.
Carroll & Ostlie. An Introduction to Modern Astrophysics, σελ. 1128-1129.
Βιβλιογραφία
Bradley W. Carroll, Dale A. Ostlie (2007). An Introduction to Modern Astrophysics. Addison-Wesley Publishing Co.. ISBN 978-960-524-206-0..
Hellenica World - Scientific Library
Από τη ελληνική Βικιπαίδεια http://el.wikipedia.org . Όλα τα κείμενα είναι διαθέσιμα υπό την GNU Free Documentation License

