.
Με τον όρο κλίση γενικά στις θετικές επιστήμες χαρακτηρίζεται η γωνία ανάμεσα σε ένα επίπεδο αναφοράς και σε ένα άλλο επίπεδο ή άξονα. Ειδικότερα ως προς τις τροχιές των ουράνιων σωμάτων στην αστρονομία, η κλίση είναι μία από τις έξι τροχιακές παραμέτρους που περιγράφουν πλήρως μία τροχιά. Στην περίπτωση των σωμάτων του Ηλιακού Συστήματος, η κλίση της τροχιάς ή τροχιακή κλίση ενός πλανήτη, κομήτη, αστεροειδούς κλπ. ορίζεται ως η γωνία ανάμεσα στο επίπεδο της τροχιάς και το επίπεδο της εκλειπτικής, δηλαδή το επίπεδο πάνω στο οποίο κείται η τροχιά της Γης γύρω από τον Ήλιο[1].Θα μπορούσε να μετράται σε σχέση με κάποιο άλλο επίπεδο, όπως αυτό του ισημερινού του Ηλίου, ή το επίπεδο της τροχιάς του Δία, αλλά η εκλειπτική είναι πιο πρακτική εκλογή για παρατηρητές που εργάζονται από τη Γη.
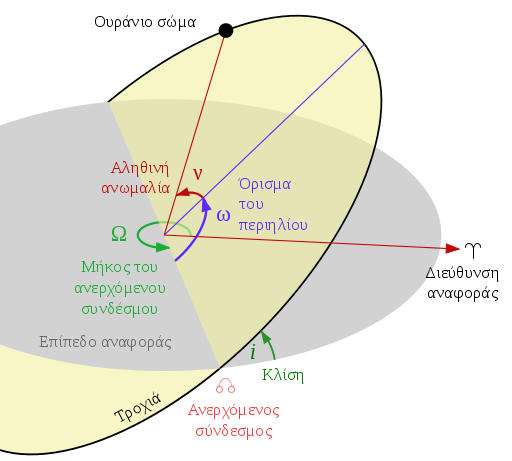
Η κλίση i (βαθύ πράσινο χρώμα) και άλλες τροχιακές παράμετροι.
Κλίσεις ηλιακού συστήματος
Οι περισσότερες πλανητικές τροχιές στο Ηλιακό Σύστημα έχουν σχετικώς μικρές κλίσεις ως προς την εκλειπτική, ως προς τα επίπεδα περιφοράς των υπόλοιπων πλανητών και ως προς τον ηλιακό ισημερινό. Αξιοσημείωτες εξαιρέσεις αποτελούν οι νάνοι πλανήτες Πλούτων και Έρις, που έχουν κλίση ως προς την εκλειπτική 17 και 44 μοιρών αντιστοίχως, ενώ από τους μεγάλους αστεροειδείς η Παλλάς έχει κλίση 34 μοιρών.
| Κλίση | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Όνομα | Inclination to Εκλειπτική |
Κλίση στον Ισημερινό του Ήλιου |
Κλίση σε αμετάβλητο επίπεδο[2] |
||||||||
| Χερσαίοι πλανήτες | Ερμής | 7.01° | 3.38° | 6.34° | |||||||
| Αφροδίτη | 3.39° | 3.86° | 2.19° | ||||||||
| Γη | 0° | 7.155° | 1.57° | ||||||||
| Άρης | 1.85° | 5.65° | 1.67° | ||||||||
| Αέριος γίγαντας | Δίας | 1.31° | 6.09° | 0.32° | |||||||
| Κρόνος | 2.49° | 5.51° | 0.93° | ||||||||
| Ουρανός | 0.77° | 6.48° | 1.02° | ||||||||
| Ποσειδώνας | 1.77° | 6.43° | 0.72° | ||||||||
Φυσικοί και τεχνητοί δορυφόροι
Η τροχιακή κλίση των φυσικών ή τεχνητών δορυφόρων μετράται ως προς το ισημερινό επίπεδο του ουράνιου σώματος γύρω από το οποίο περιφέρονται, εάν δεν περιφέρονται αρκετά μακριά από αυτό. Το ισημερινό επίπεδο είναι το επίπεδο που είναι κάθετο στον άξονα περιστροφής του κεντρικού σώματος.
- Κλίση 0 μοιρών σημαίνει ότι ο δορυφόρος περιφέρεται πάνω στο ισημερινό επίπεδο του πλανήτη (ισημερινή τροχιά) και κατά τη φορά περιστροφής του ίδιου του πλανήτη.
- Κλίση μεγαλύτερη των -90° και μικρότερη των 90° αντιστοιχεί σε κίνηση του δορυφόρου κατά την ορθή φορά.
- Κλίση μεγαλύτερη των 90° και μικρότερη των 270° αντιστοιχεί σε κίνηση του δορυφόρου κατά την ανάδρομη φορά.
- Κλίση ίση με 90° αντιστοιχεί σε μία πολική τροχιά, στην οποία ο δορυφόρος (ή το διαστημόπλοιο) περνά ακριβώς πάνω από τους δύο πόλους του πλανήτη σε κάθε περιφορά του.
- Κλίση ίση με 180° αντιστοιχεί σε μία ανάδρομη ισημερινή τροχιά.
Για τη Σελήνη, η μέτρηση της κλίσεως της τροχιάς της γύρω από τη Γη ως προς το ισημερινό επίπεδο του πλανήτη μας οδηγεί σε μία τιμή που μεταβάλλεται γρήγορα. Είναι πιο λογική η μέτρησή της ως προς ττην εκλειπτική (δηλ. το επίπεδο της τροχιάς του συστήματος Γη-Σελήνη γύρω από τον `Ηλιο), που είναι μία αρκετά σταθερή ποσότητα.
Εξωηλιακοί πλανήτες και πολλαπλά αστρικά συστήματα
Η κλίση εξωηλιακών πλανητών ή μελών πολλαπλών αστέρων είναι η γωνία που σχηματίζει το επίπεδο της τροχιάς τους με το επίπεδο που είναι κάθετο στην ευθεία που ενώνει τον παρατηρητή με το συγκεκριμένο σώμα.
- Κλίση 0 μοιρών αντιστοιχεί σε τροχιά κατά την ορθή φορά που την παρατηρούμε σε κάτοψη (δηλαδή το επίπεδο της τροχιάς είναι παράλληλο με τον ουρανό).
- Κλίση μεγαλύτερη των 0° και μικρότερη των 90° αντιστοιχεί σε τροχιά κατά την ορθή φορά, που είναι η φορά περιστροφής του κεντρικού ή του κύριου αστέρα.
- Κλίση ίση με 90° αντιστοιχεί σε τροχιά πάνω στο επίπεδο που περιλαμβάνει τον παρατηρητή, ανεξάρτητα από το αν η τροχιά είναι κατά την ορθή ή κατά την ανάδρομη φορά.
- Κλίση μεγαλύτερη των 90° και μικρότερη των 180° αντιστοιχεί σε τροχιά κατά την ανάδρομη φορά, δηλαδή αντίθετα από τη φορά περιστροφής του κεντρικού ή του κύριου αστέρα.
- Κλίση ίση με 180° αντιστοιχεί σε τροχιά κατά την ανάδρομη φορά που την παρατηρούμε σε κάτοψη.
Επειδή η μέθοδος της ακτινικής ταχύτητας είναι ευκολότερο να βρει πλανήτες με μεγάλες κλίσεις, οι περισσότεροι εξωηλιακοί πλανήτες που ανακαλύφθηκαν μέχρι σήμερα θα έχουν κλίσεις μεταξύ 45° και 135°, παρότι οι περισσότεροι δεν έχουν γνωστές κλίση. Αντιστοίχως, οι περισσότεροι εξωηλιακοί πλανήτες θα έχουν πραγματικές μάζες όχι μεγαλύτερες από 1,7 φορά την υπολογιζόμενη ελάχιστη μάζα τους. Αν η κλίση είναι κοντά στις 90°, τότε ο πλανήτης πιθανότατα μπορεί να παρατηρηθεί να περνά μπροστά από τον κεντρικό του αστέρα. Αν η τροχιακή κλίση είναι σχεδόν 0, ιδιαίτερα για πλανήτες με μάζες μεγαλύτερες εκείνης του Δία που ανακαλύπτονται με τη μέθοδο της ακτινικής ταχύτητας, τότε αυτά τα σώματα μπορεί στην πραγματικότητα να είναι φαιοί νάνοι ή ακόμα και ερυθροί νάνοι: π.χ. ο HD 33636 B έχει πραγματική μάζα 142 μάζες Δία, που αντιστοιχεί σε αστέρα τύπου M6 V, ενώ η ελάχιστη μάζα που υπολογίζεται γι' αυτόν είναι 9,28 μάζες Δία. Οι κλίσεις και επομένως οι ακριβείς μάζες για σχεδόν όλους τους εξωηλιακούς πλανήτες που έχουν ανακαλυφθεί θα μετρηθούν τελικώς με τη βοήθεια διαστημικών αποστολών, όπως η Αποστολή Gaia, η Αποστολή Διαστημικής Συμβολομετρίας (Space Interferometry Mission, SIM) και το Διαστημικό Τηλεσκόπιο Τζέιμς Γουέμπ.
`Αλλες σημασίες
Για πλανήτες και άλλα περιστρεφόμενα ουράνια σώματα, η γωνία του άξονα περιστροφής με την κάθετο στο επίπεδο της τροχιάς επίσης αποκαλείται κάποτε κλίση ή αξονική κλίση, αλλά για την αποφυγή συγχύσεων μπορεί να αποκαλείται λόξωση.
Υπολογισμός
Στην αστροδυναμική η κλίση i μπορεί να υπολογισθεί από το διάνυσμα της τροχιακής στροφορμής \mathbf{h}\, (ή οποιοδήποτε άλλο διάνυσμα κάθετο στο επίπεδο της τροχιάς:
i=\arccos{h_\mathrm{z}\over\left|\mathbf{h}\right|},
όπου h_\mathrm{z} είναι η z-συνιστώσα της \mathbf{h}.
Η αμοιβαία κλίση δύο τροχιών μπορεί να υπολογισθεί από τις κλίσεις τους ως προς ένα άλλο επίπεδο με χρήση του σφαιρικού νόμου των συνημιτόνων.
Δείτε επίσης
Λόξωση
Αζιμούθιο
Κεπλέρεια τροχιά
Φαινόμενο Κοζάι
Σημειώσεις
McBride, Neil; Bland, Philip A.; Gilmour, Iain (2004). An Introduction to the Solar System. Cambridge University Press, σελ. 248. ISBN 0-521-54620-6.
«The MeanPlane (Invariable plane) of the Solar System passing through the barycenter». 2009-04-03. Ανακτήθηκε στις 2009-04-10. (produced with Solex 10 written by Aldo Vitagliano)
Στο λήμμα αυτό έχει ενσωματωθεί κείμενο από το λήμμα Orbital inclination της Αγγλικής Βικιπαίδειας, η οποία διανέμεται υπό την GNU FDL και την CC-BY-SA 3.0. (ιστορικό/συντάκτες).
Hellenica World - Scientific Library
Από τη ελληνική Βικιπαίδεια http://el.wikipedia.org . Όλα τα κείμενα είναι διαθέσιμα υπό την GNU Free Documentation License