Mathematische Spuren

Archimedes, drawing geometric figures in the sand.

Dont disturb my circles
Archimedes last words, while he was drawing geometric figures on the sand, before he was killed by a roman soldier. According to William Rankin ( “Introducing Newton” Totem Books) the only appearance of a Roman in the history of Mathematics.

Aristippus a Philosopher with others shipwrecked on the shores of the island Rhodes. They do not know where they are, if the island is inhabited. Aristippus observes geometric figures drawn on the sand. His comment: There is hope, I see traces of men. Actually of educated men since Rhodes was a technological advanced place (for example we have Hipparchus of Rhodes, Posidonius with his astronomic measurements in Rhodes and devices like the repeating catapult of Dionysius of Alexandria who worked in Rhodes or the Colossus of Rhodes or the Antikythera mechanism.

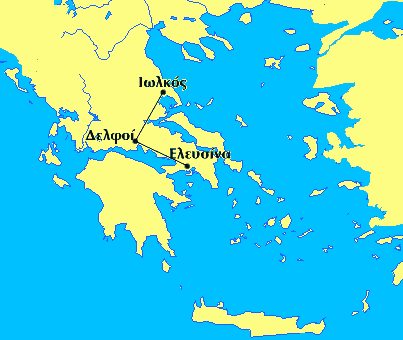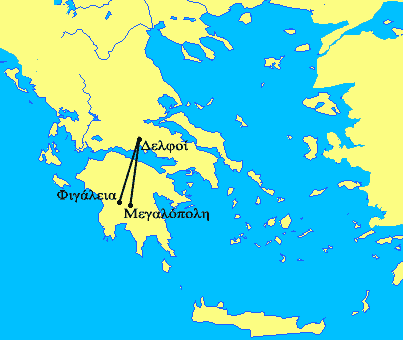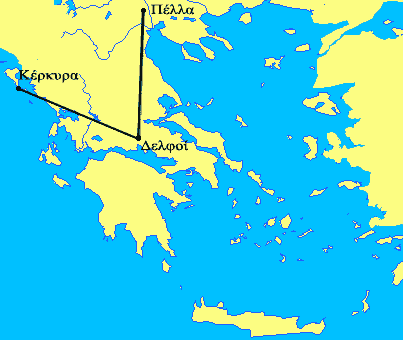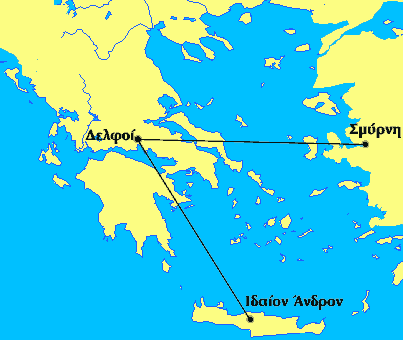
The Mystery of Ley Lines (a connection to String theory???)

According to Mythology Delphi was the centre of the world that Zeus determined by two eagles which flew from Mount Olympus in opposite directions and met at a point in Delphi marked by Zeus with the omphalos ("navel") stone which his mother Rhea had wrapped with clothes to take Zeus place and fool Kronos, his father. This is a strange story since I don't know how this method determines a center, how this center is defined and what did Zeus assume about the shape of the Earth. More logical we can assume that Delphi is at the same distance from Olympus in two opposite directions. A better explanation is the story that the eagles started at the opposite ends of the world and not from Olympus.

Some suggest that the position of special places like Delphi in ancient Greece have been selected based on geometrical principles. For example at least 6 pairs of cities are mentioned that are at an equal distance to Delphi. One such pair is Athens and Olympia. Does this mean that the Greeks designed the position of Delphi on the basis of the position of other cities? If yes this is an interesting mathematical problem. Is it possible to find 6 (and why not even more?) such pairs of places that are at equal distance to Delphi? I think this is possible (which depends on how accurate the distance is measured). But even if it would be difficult to find such places why these pairs of cities have been selected by the ancient Greeks? When was Delphi build in relation to the other places? Even if Delphi is not the only place but other places can be found like Dodona and Delos I don't think that this is a proof that the position of some cities were choosen based on geometry (“sacred geometry”).