ART

In geometry, a honeycomb is a space filling or close packing of polyhedral or higher-dimensional cells, so that there are no gaps. It is an example of the more general mathematical tiling or tessellation in any number of dimensions. Its dimension can be clarified as n-honeycomb for a honeycomb of n-dimensional space.

Honeycombs are usually constructed in ordinary Euclidean ("flat") space. They may also be constructed in non-Euclidean spaces, such as hyperbolic honeycombs. Any finite uniform polytope can be projected to its circumsphere to form a uniform honeycomb in spherical space.
It is possible to fill the plane with polygons which do not meet at their corners, for example using rectangles, as in a brick wall pattern: this is not a proper tiling because corners lie part way along the edge of a neighbouring polygon. Similarly, in a proper honeycomb, there must be no edges or vertices lying part way along the face of a neighbouring cell. Interpreting each brick face as a hexagon having two interior angles of 180 degrees allows the pattern to be considered as a proper tiling. However, not all geometers accept such hexagons.

Classification

There are infinitely many honeycombs, which have only been partially classified. The more regular ones have attracted the most interest, while a rich and varied assortment of others continue to be discovered.

The simplest honeycombs to build are formed from stacked layers or slabs of prisms based on some tessellations of the plane. In particular, for every parallelepiped, copies can fill space, with the cubic honeycomb being special because it is the only regular honeycomb in ordinary (Euclidean) space. Another interesting family is the Hill tetrahedra and their generalizations, which can also tile the space.

Uniform 3-honeycombs

A 3-dimensional uniform honeycomb is a honeycomb in 3-space composed of uniform polyhedral cells, and having all vertices the same (i.e., the group of [isometries of 3-space that preserve the tiling] is transitive on vertices). There are 28 convex examples in Euclidean 3-space,[1] also called the Archimedean honeycombs.

A honeycomb is called regular if the group of isometries preserving the tiling acts transitively on flags, where a flag is a vertex lying on an edge lying on a face lying on a cell. Every regular honeycomb is automatically uniform. However, there is just one regular honeycomb in Euclidean 3-space, the cubic honeycomb. Two are quasiregular (made from two types of regular cells):

Type Regular cubic honeycomb Quasiregular honeycombs
Cells Cubic Octahedra and tetrahedra
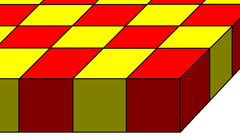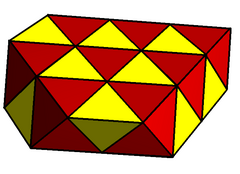Slab layer Cubic semicheck.png Tetroctahedric semicheck.png

The tetrahedral-octahedral honeycomb and gyrated tetrahedral-octahedral honeycombs are generated by 3 or 2 positions of slab layer of cells, each alternating tetrahedra and octahedra. An infinite number of unique honeycombs can be created by higher order of patterns of repeating these slab layers.

Space-filling polyhedra
See also: Stereohedron, Plesiohedron, and Parallelohedron

A honeycomb having all cells identical within its symmetries is said to be cell-transitive or isochoric. In the 3-dimensional euclidean space, a cell of such a honeycomb is said to be a space-filling polyhedron.[2] A necessary condition for a polyhedron to be a space-filling polyhedron is that its Dehn invariant must be zero,[3][4] ruling out any of the Platonic solids other than the cube.

Five space-filling polyhedra can tessellate 3-dimensional euclidean space using translations only. They are called parallelohedra:

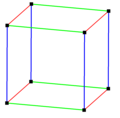
Cubic honeycomb (or variations: cuboid, rhombic hexahedron or parallelepiped)
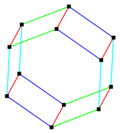
Hexagonal prismatic honeycomb[5]
Rhombic dodecahedral honeycomb
Elongated dodecahedral honeycomb.[6]
Bitruncated cubic honeycomb or truncated octahedra[7]

Rhombohedral prism honeycomb.png
cubic honeycomb		 Skew hexagonal prism honeycomb.png
Hexagonal prismatic honeycomb		 Rhombic dodecahedra.png
Rhombic dodecahedra		 Elongated rhombic dodecahedron honeycomb.png
Elongated dodecahedra		 Truncated octahedra.png
Truncated octahedra
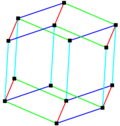
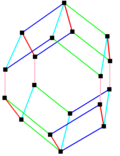
Cube
(parallelepiped)		 Hexagonal prism Rhombic dodecahedron Elongated dodecahedron Truncated octahedron
Parallelohedron edges cube.png Parallelohedron edges hexagonal prism.png Parallelohedron edges rhombic dodecahedron.png Parallelohedron edges elongated rhombic dodecahedron.png Parallelohedron edge truncated octahedron.png
3 edge-lengths 3+1 edge-lengths 4 edge-lengths 4+1 edge-lengths 6 edge-lengths

Other known examples of space-filling polyhedra include:

The Triangular prismatic honeycomb.
The gyrated triangular prismatic honeycomb
The triakis truncated tetrahedral honeycomb. The Voronoi cells of the carbon atoms in diamond are this shape.[8]
The trapezo-rhombic dodecahedral honeycomb[9]
Isohedral tilings.[10]

Other honeycombs with two or more polyhedra

Sometimes, two [11] or more different polyhedra may be combined to fill space. Besides many of the uniform honeycombs, another well known example is the Weaire–Phelan structure, adopted from the structure of clathrate hydrate crystals [12]

12-14-hedral honeycomb.png

12-14-hedral honeycomb

Weaire–Phelan structure (With two types of cells)
Non-convex 3-honeycombs

Documented examples are rare. Two classes can be distinguished:

Non-convex cells which pack without overlapping, analogous to tilings of concave polygons. These include a packing of the small stellated rhombic dodecahedron, as in the Yoshimoto Cube.
Overlapping of cells whose positive and negative densities 'cancel out' to form a uniformly dense continuum, analogous to overlapping tilings of the plane.

Hyperbolic honeycombs

In 3-dimensional hyperbolic space, the dihedral angle of a polyhedron depends on its size. The regular hyperbolic honeycombs thus include two with four or five dodecahedra meeting at each edge; their dihedral angles thus are π/2 and 2π/5, both of which are less than that of a Euclidean dodecahedron. Apart from this effect, the hyperbolic honeycombs obey the same topological constraints as Euclidean honeycombs and polychora.

The 4 compact and 11 paracompact regular hyperbolic honeycombs and many compact and paracompact uniform hyperbolic honeycombs have been enumerated.

Four regular compact honeycombs in H3
H3 534 CC center.png
{5,3,4}		 H3 435 CC center.png
{4,3,5}		 H3 353 CC center.png
{3,5,3}		 H3 535 CC center.png
{5,3,5}
11 paracompact regular honeycombs
H3 633 FC boundary.png
{6,3,3}		 H3 634 FC boundary.png
{6,3,4}		 H3 635 FC boundary.png
{6,3,5}		 H3 636 FC boundary.png
{6,3,6}		 H3 443 FC boundary.png
{4,4,3}		 H3 444 FC boundary.png
{4,4,4}
H3 336 CC center.png
{3,3,6}		 H3 436 CC center.png
{4,3,6}		 H3 536 CC center.png
{5,3,6}		 H3 363 FC boundary.png
{3,6,3}		 H3 344 CC center.png
{3,4,4}

Duality of 3-honeycombs

For every honeycomb there is a dual honeycomb, which may be obtained by exchanging:

cells for vertices.
faces for edges.

These are just the rules for dualising four-dimensional 4-polytopes, except that the usual finite method of reciprocation about a concentric hypersphere can run into problems.

The more regular honeycombs dualise neatly:

The cubic honeycomb is self-dual.
That of octahedra and tetrahedra is dual to that of rhombic dodecahedra.
The slab honeycombs derived from uniform plane tilings are dual to each other in the same way that the tilings are.
The duals of the remaining Archimedean honeycombs are all cell-transitive and have been described by Inchbald.[13]

Self-dual honeycombs

Honeycombs can also be self-dual. All n-dimensional hypercubic honeycombs with Schläfli symbols {4,3n−2,4}, are self-dual.
See also
List of uniform tilings
Regular honeycombs
Infinite skew polyhedron
Plesiohedron

References

Grünbaum (1994). "Uniform tilings of 3-space". Geombinatorics 4(2)
Weisstein, Eric W. "Space-filling polyhedron". MathWorld.
Debrunner, Hans E. (1980), "Über Zerlegungsgleichheit von Pflasterpolyedern mit Würfeln", Archiv der Mathematik (in German), 35 (6): 583–587, doi:10.1007/BF01235384, MR 0604258.
Lagarias, J. C.; Moews, D. (1995), "Polytopes that fill R n {\displaystyle \mathbb {R} ^{n}} \mathbb {R} ^{n} and scissors congruence", Discrete and Computational Geometry, 13 (3–4): 573–583, doi:10.1007/BF02574064, MR 1318797.
[1] Uniform space-filling using triangular, square, and hexagonal prisms
[2] Uniform space-filling using only rhombo-hexagonal dodecahedra
[3] Uniform space-filling using only truncated octahedra
John Conway (2003-12-22). "Voronoi Polyhedron. geometry.puzzles". Newsgroup: geometry.puzzles. Usenet: Pine.LNX.4.44.0312221226380.25139-100000@fine318a.math.Princeton.EDU.
X. Qian, D. Strahs and T. Schlick, J. Comput. Chem. 22(15) 1843–1850 (2001)
[4] O. Delgado-Friedrichs and M. O'Keeffe. Isohedral simple tilings: binodal and by tiles with <16 faces. Acta Crystallogr. (2005) A61, 358-362
[5] Archived 2015-06-30 at the Wayback Machine Gabbrielli, Ruggero. A thirteen-sided polyhedron which fills space with its chiral copy.
Pauling, Linus. The Nature of the Chemical Bond. Cornell University Press, 1960

Inchbald, Guy (July 1997), "The Archimedean honeycomb duals", The Mathematical Gazette, 81 (491): 213–219, doi:10.2307/3619198, JSTOR 3619198.

Further reading

Coxeter, H. S. M.: Regular Polytopes.
Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. pp. 164–199. ISBN 0-486-23729-X. Chapter 5: Polyhedra packing and space filling
Critchlow, K.: Order in space.
Pearce, P.: Structure in nature is a strategy for design.
Goldberg, Michael Three Infinite Families of Tetrahedral Space-Fillers Journal of Combinatorial Theory A, 16, pp. 348–354, 1974.
Goldberg, Michael (1972). "The space-filling pentahedra". Journal of Combinatorial Theory, Series A. 13 (3): 437–443. doi:10.1016/0097-3165(72)90077-5.
Goldberg, Michael The Space-filling Pentahedra II, Journal of Combinatorial Theory 17 (1974), 375–378.
Goldberg, Michael (1977). "On the space-filling hexahedra". Geometriae Dedicata. 6. doi:10.1007/BF00181585.
Goldberg, Michael (1978). "On the space-filling heptahedra". Geometriae Dedicata. 7 (2): 175–184. doi:10.1007/BF00181630.
Goldberg, Michael Convex Polyhedral Space-Fillers of More than Twelve Faces. Geometriae Dedicata 8, 491-500, 1979.
Goldberg, Michael (1981). "On the space-filling octahedra". Geometriae Dedicata. 10 (1–4): 323–335. doi:10.1007/BF01447431.
Goldberg, Michael (1982). "On the Space-filling Decahedra".
Goldberg, Michael (1982). "On the space-filling enneahedra". Geometriae Dedicata. 12 (3). doi:10.1007/BF00147314.

External links

Olshevsky, George. "Honeycomb". Glossary for Hyperspace. Archived from the original on 4 February 2007.
Five space-filling polyhedra, Guy Inchbald, The Mathematical Gazette 80, November 1996, p.p. 466-475.
Raumfueller (Space filling polyhedra) by T.E. Dorozinski
Weisstein, Eric W. "Space-Filling Polyhedron". MathWorld.

Fundamental convex regular and uniform honeycombs in dimensions 2-9
Space Family \( {\tilde {A}}_{n-1} \) \( {\tilde {C}}_{n-1} \) \( {\tilde {B}}_{n-1} \) \( {\tilde {D}}_{n-1} \) \( {\tilde {G}}_{2} / {\tilde {F}}_{4} / {\tilde {E}}_{n-1} \)
E2 Uniform tiling {3[3]} δ3 hδ3 qδ3 Hexagonal
E3 Uniform convex honeycomb {3[4]} δ4 hδ4 qδ4
E4 Uniform 4-honeycomb {3[5]} δ5 hδ5 qδ5 24-cell honeycomb
E5 Uniform 5-honeycomb {3[6]} δ6 hδ6 qδ6
E6 Uniform 6-honeycomb {3[7]} δ7 hδ7 qδ7 222
E7 Uniform 7-honeycomb {3[8]} δ8 hδ8 qδ8 133 • 331
E8 Uniform 8-honeycomb {3[9]} δ9 hδ9 qδ9 152 • 251 • 521
E9 Uniform 9-honeycomb {3[10]} δ10 hδ10 qδ10
En-1 Uniform (n-1)-honeycomb {3[n]} δn hδn qδn 1k2 • 2k1 • k21

Undergraduate Texts in Mathematics

Graduate Texts in Mathematics

Graduate Studies in Mathematics

Mathematics Encyclopedia

World

Index

Hellenica World - Scientific Library

Retrieved from "http://en.wikipedia.org/"
All text is available under the terms of the GNU Free Documentation License