Amoeba (mathematics)

In complex analysis, a branch of mathematics, an amoeba is a set associated with a polynomial in one or more complex variables. Amoebas have applications in algebraic geometry, especially tropical geometry.

Definition

Consider the function

\( {\displaystyle \operatorname {Log} :{\big (}{\mathbb {C} }\setminus \{0\}{\big )}^{n}\to \mathbb {R} ^{n}} \)

defined on the set of all n-tuples \( {\displaystyle z=(z_{1},z_{2},\dots ,z_{n})} \) of non-zero complex numbers with values in the Euclidean space \( \mathbb {R} ^{n} \), given by the formula

\( {\displaystyle \operatorname {Log} (z_{1},z_{2},\dots ,z_{n})={\big (}\log |z_{1}|,\log |z_{2}|,\dots ,\log |z_{n}|{\big )}.} \)

Here, log denotes the natural logarithm. If p(z) is a polynomial in n {\displaystyle n} n complex variables, its amoeba \( {\displaystyle {\mathcal {A}}_{p}} \) is defined as the image of the set of zeros of p under Log, so

\( {\displaystyle {\mathcal {A}}_{p}=\left\{\operatorname {Log} (z):z\in {\big (}\mathbb {C} \setminus \{0\}{\big )}^{n},p(z)=0\right\}.} \)

Amoebas were introduced in 1994 in a book by Gelfand, Kapranov, and Zelevinsky.[1]

The amoeba of P(z, w) = w − 2z − 1

The amoeba of P(z, w) = 3z² + 5zw + w³ + 1. Notice the "vacuole" in the middle of the amoeba.

Properties

Any amoeba is a closed set.
Any connected component of the complement \( {\displaystyle \mathbb {R} ^{n}\setminus {\mathcal {A}}_{p}} \) is convex.[2]
The area of an amoeba of a not identically zero polynomial in two complex variables is finite.
A two-dimensional amoeba has a number of "tentacles", which are infinitely long and exponentially narrow towards infinity.

Ronkin function

The amoeba of P(z, w) = 1 + z + z² + z³ + z²w³ + 10zw + 12z²w + 10z²w²

The amoeba of P(z, w) = 50z³ + 83z²w + 24zw² + w³ + 392z² + 414zw + 50w² − 28z + 59w − 100

A useful tool in studying amoebas is the Ronkin function. For p(z), a polynomial in n complex variables, one defines the Ronkin function

\( {\displaystyle N_{p}:\mathbb {R} ^{n}\to \mathbb {R} } \)

by the formula

\( {\displaystyle N_{p}(x)={\frac {1}{(2\pi i)^{n}}}\int _{\operatorname {Log} ^{-1}(x)}\log |p(z)|\,{\frac {dz_{1}}{z_{1}}}\wedge {\frac {dz_{2}}{z_{2}}}\wedge \cdots \wedge {\frac {dz_{n}}{z_{n}}},} \)

where x denotes \( {\displaystyle x=(x_{1},x_{2},\dots ,x_{n}).} \) Equivalently, \( N_{p} \) is given by the integral

\( {\displaystyle N_{p}(x)={\frac {1}{(2\pi )^{n}}}\int _{[0,2\pi ]^{n}}\log |p(z)|\,d\theta _{1}\,d\theta _{2}\cdots d\theta _{n},} \)

where

\( {\displaystyle z=\left(e^{x_{1}+i\theta _{1}},e^{x_{2}+i\theta _{2}},\dots ,e^{x_{n}+i\theta _{n}}\right).} \)

The Ronkin function is convex and affine on each connected component of the complement of the amoeba of p p(z).[3]

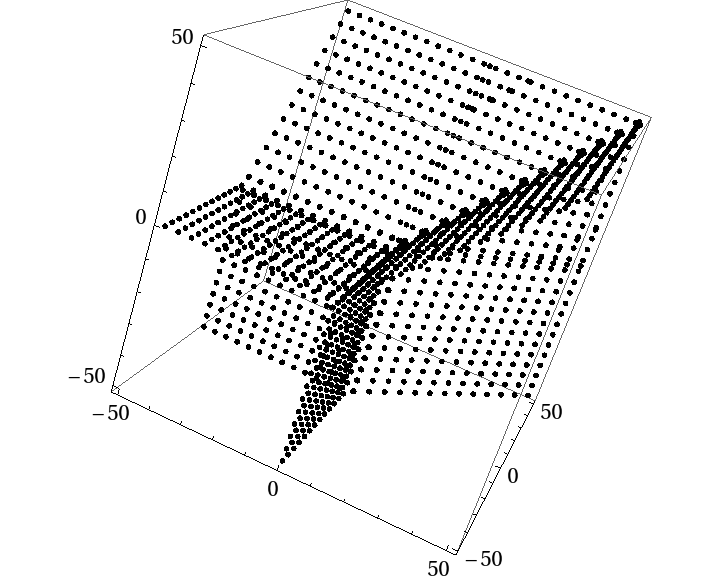
Points in the amoeba of P(x, y, z) = x + y + z − 1. Note that the amoeba is actually 3-dimensional, and not a surface (this is not entirely evident from the image).

As an example, the Ronkin function of a monomial

\( {\displaystyle p(z)=az_{1}^{k_{1}}z_{2}^{k_{2}}\dots z_{n}^{k_{n}}} \)

with \( a\neq 0 \) is

\({\displaystyle N_{p}(x)=\log |a|+k_{1}x_{1}+k_{2}x_{2}+\cdots +k_{n}x_{n}.} \)

References

Gelfand, I. M.; Kapranov, M. M.; Zelevinsky, A. V. (1994). Discriminants, resultants, and multidimensional determinants. Mathematics: Theory & Applications. Boston, MA: Birkhäuser. ISBN 0-8176-3660-9. Zbl 0827.14036.
Itenberg et al (2007) p. 3.

Gross, Mark (2004). "Amoebas of complex curves and tropical curves". In Guest, Martin (ed.). UK-Japan winter school 2004—Geometry and analysis towards quantum theory. Lecture notes from the school, University of Durham, Durham, UK, 6–9 January 2004. Seminar on Mathematical Sciences. 30. Yokohama: Keio University, Department of Mathematics. pp. 24–36. Zbl 1083.14061.

Itenberg, Ilia; Mikhalkin, Grigory; Shustin, Eugenii (2007). Tropical algebraic geometry. Oberwolfach Seminars. 35. Basel: Birkhäuser. ISBN 978-3-7643-8309-1. Zbl 1162.14300.
Viro, Oleg (2002), "What Is ... An Amoeba?" (PDF), Notices of the American Mathematical Society, 49 (8): 916–917.